为了复习数据结构实验考试，将OJ题目再过一遍吧…不要问我为什么大三才考这个，这就是转专业的魅力~~

实验一

问题 A: 判断三角形形状

题目描述

给你三角形的三条边，你能告诉我它是哪种三角形吗？
如果是直角三角形，请输出“good”。如果是等腰三角形，请输出“perfect”。否则，请输出“just a triangle”。
题目保证输入数据合法。

输入

输入的第一行为一个整数t，表示测试样例的数量。
每组样例包含了三个整数a,b,c，代表了三角形的三条边的长度。（0<a,b,c<300）

输出

对于每组样例，输出结果，每组结果占一行。
样例输入

1
2
3
4
5
4
3 4 5
2 2 3 
1 4 4
4 6 3
样例输出
1
2
3
4
good
perfect
perfect
just a triangle
思路

没啥好说的，基础题

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
#include<string>
using namespace std;
string Judge(int x, int y, int z)
{
	string type = "just a triangle";
	if (x == y || x == z || y == z)
		type = "perfect";
	else if (x*x == y * y + z * z || x * x + y * y == z * z || x * x + z * z == y * y)
		type = "good";
	return type;
}
int main()
{
	int x, y, z;
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> x >> y >> z;
		cout << Judge(x, y, z) << endl;
	}
	return 0;
}

问题 B: 笨鸟先飞

题目描述

多多是一只小菜鸟，都说笨鸟先飞，多多也想来个菜鸟先飞。于是它从0点出发，一开始的飞行速度为1m/s，每过一个单位时间多多的飞行速度比上一个单位时间的飞行速度快2m/s，问n（0<n<10^5）个单位时间之后多多飞了多远?

输入

先输入一个整数T表示有几组数据。每组数据输入一个n，表示多多飞行的时间。

输出

输出多多飞行了多远，因为数字很大，所以对10000取模。

样例输入
1
2
3
2
1
2
样例输出
1
2
1
4
思路

第i+1个单位时间的速度为1+2*i，累和一下就行了，注意要模10000取余

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
using namespace std;
int t;
int main()
{
	int n;
	cin >> t;
	while (t--)
	{
		cin >> n;
		int sum = 0;
		for (int i = 0; i < n; i++)
		{
			sum += (1 + 2 * i) % 10000;
		}
		cout << sum % 10000 << endl;
	}
	return 0;
}


问题 C: 火车出站*

题目描述

铁路进行列车调度时，常把站台设计成栈式结构的站台，试问：
设有编号为1到n的n辆列车，顺序开入栈式结构的站台，则可能的出栈序列有多少种？

输入

输入包含多组测试数据。每组为一个正整数n（1<=n<=20），表示有n辆列车。

输出

输出可能的出栈序列有多少种。

样例输入
1
2
4
3
样例输出
1
2
14
5
思路

火车出栈问题，书上给出了公式，带公式即可。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# include <iostream>
using namespace std;
int main()
{
	long long int t[20]; 
	t[0] = 1;
	for (int i = 1; i <= 20; i++)
	{
		t[i] = t[i - 1] * (4 * i - 2) / (i + 1);
	}
	int n;
	while (cin >> n)
	{
		cout << t[n] << endl;
	}
	return 0;
}

问题 D: 最少的交换*

题目描述

现在给你一个由n个互不相同的整数组成的序列，现在要求你任意交换相邻的两个数字，使序列成为升序序列，请问最少的交换次数是多少？

输入

输入包含多组测试数据。每组输入第一行是一个正整数n（n<500000），表示序列的长度，当n=0时。
接下来的n行，每行一个整数a[i]（0<=a[i]<=999999999），表示序列中第i个元素。

输出

对于每组输入，输出使得所给序列升序的最少交换次数。

样例输入
1
2
3
4
5
6
7
8
9
10
11
5
9
1
0
5
4
3
1
2
3
0
样例输出
1
2
6
0
思路

利用归并排序，将已有序的子序列合并，得到完全有序的序列，即用分治法解决。

先使每个子序列（前半部分和后半部分）有序，再使子序列段间有序，前后两部分两两比较，将两个有序表合并成一个有序表。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<iostream>
using namespace std;
long long sum;
int a[500010], b[500010];
//将两个有序表合并为一个有序表
void Merge(int a[], int low, int mid, int high)
{
	int i = low, j = mid + 1, k = low;
	while (i <= mid && j <= high)
	{
		if (a[i] <= a[j])
		{
			b[k++] = a[i++];
		}
		else
		{
			sum += j - k;	// 每当后段的数组元素提前时，记录提前的距离
			b[k++] = a[j++];
		}
	}
	while (i <= mid)		//若左半部分还有剩余
	{
		b[k++] = a[i++];	
	}
	while (j <= high)		//若右半部分还有剩余
	{
		b[k++] = a[j++];
	}
	for (i = low; i <= high; i++)
	{
		a[i] = b[i];
	} 
}
void MergeSort(int a[], int low, int high)
{
	if (low < high)
	{
		int mid = (low + high) / 2;
		MergeSort(a, low, mid);			//使左半部分有序
		MergeSort(a, mid + 1, high);	//使右半部分有序
		Merge(a, low, mid, high);		//进行归并
	}
}

int main()
{
	int n;
	while (cin >> n)
	{
		if (n == 0)
			break;
		sum = 0;
		for (int i = 0; i < n; i++)
		{
			cin >> a[i];
		}
		MergeSort(a, 0, n - 1);
		cout << sum << endl;
	}
	return 0;
}

问题 E: 欧几里得游戏

题目描述

小明和小红在玩欧几里得游戏。他们从两个自然数开始，第一个玩家小明，从两个数的较大数中减去较小数的尽可能大的正整数倍，只要差为非负即可。然后，第二个玩家小红，对得到的两个数进行同样的操作，然后又是小明。就这样轮流进行游戏，直至某个玩家将较大数减去较小数的某个倍数之后差为0为止，此时游戏结束，该玩家就是胜利者。

输入

输入包含多组测试数据。每组输入两个正整数，表示游戏一开始的两个数，游戏总是小明先开始。
当输入两个0的时候，输入结束。

输出

对于每组输入，输出最后的胜者，我们认为他们两个都是顶尖高手，每一步游戏都做出了最佳的选择。
具体输出格式见输出样例。

样例输入
1
2
3
34 12
15 24
0 0
样例输出
1
2
xiaoming wins
xiaohong wins
思路

关于博弈论的一道题，有点难…

参考这篇文章：https://blog.csdn.net/winter2121/article/details/81950819

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
using namespace std;
int main()
{
	int a, b;
	int count;
	while (cin >> a >> b)
	{
		if (a == 0 || b == 0)
			break;
		count = 1;
		if (a == b)
			cout << "xiaoming wins" << endl;
		else
		{
			while (a != b)
			{
				if (a < b)	
				{
					int temp = a;
					a = b;
					b = temp;
				}
				count++;
				if (a / b != 1)
					break;
				a = a % b;
			}
			if (count % 2 == 1)
				cout << "xiaohong wins" << endl;
			else
				cout << "xiaoming wins" << endl;
		}
	}
	return 0;
}

问题 F: 取石子游戏

题目描述

一天小明和小红在玩取石子游戏，游戏规则是这样的：
（1）本游戏是一个二人游戏；
（2）有一堆石子，共有n个；
（3）两人轮流进行；
（4）每走一步可以取走1~m个石子；
（5）最先取光石子的一方为胜。
如果游戏的双方使用的都是最优策略，请输出哪个人能赢。

输入

输入的第一行是一个正整数C（C<=100），表示有C组测试数据。
每组输入两个整数n和m（1<=n,m<=1000），n和m的含义见题目描述。

输出

对于每组输入，如果先走的人能赢，请输出“first”，否则请输出“second”。

样例输入
1
2
3
2
23 2
4 3
样例输出
1
2
first
second
思路

巴什博奕问题

  • 如果n=m+1，由于一次最多只能取m个，所以，无论先取者拿走多少个，后取者都能够一次拿走剩余的物品，后者取胜。

  • 因此如果n=（m+1）r+s，（r为任意自然数，s≤m),那么先取者要拿走s个物品，如果后取者拿走k（≤m)个，那么先取者再拿走m+1-k个，结果剩下（m+1）（r-1）个，以后保持这样的取法，那么先取者肯定获胜。

  • 总之，要保持给对手留下（m+1）的倍数，就能最后获胜，即若n使m+1的倍数，则后取着胜，反之，存在先取者获胜的取法。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<iostream>
using namespace std;
int main()
{
	int c, n, m;
	cin >> c;
	for (int i = 0; i < c; i++)
	{
		cin >> n >> m;
		if (n % (m + 1) != 0)
			cout << "first" << endl;
		else
			cout << "second" << endl;
	}
	return 0;
}


问题 G: 奥运排序问题

题目描述

按要求，给国家进行排名。

输入

有多组数据。
第一行给出国家数N，要求排名的国家数M，国家号从0到N-1。
第二行开始的N行给定国家或地区的奥运金牌数，奖牌数，人口数（百万）。
接下来一行给出M个国家号。

输出

排序有4种方式: 金牌总数 奖牌总数 金牌人口比例 奖牌人口比例
对每个国家给出最佳排名排名方式 和 最终排名
格式为: 排名:排名方式
如果有相同的最终排名，则输出排名方式最小的那种排名，对于排名方式，金牌总数 < 奖牌总数 < 金牌人口比例 < 奖牌人口比例
如果有并列排名的情况，即如果出现金牌总数为 100,90,90,80.则排名为1,2,2,4.
每组数据后加一个空行。

样例输入
1
2
3
4
5
6
7
8
9
10
11
12
4 4
4 8 1
6 6 2
4 8 2
2 12 4
0 1 2 3
4 2
8 10 1
8 11 2
8 12 3
8 13 4
0 3
样例输出
1
2
3
4
5
6
7
1:3
1:1
2:1
1:2

1:1
1:1
思路

利用sort()按四种排名方式分别对需要排名的国家进行排名，并记录在一个二维数组中，

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <iostream>
#include <algorithm>

using namespace std;

const int s = 1005;

class Country {
public:
	double g, j, p;
	int id;
}c[s];

bool cmpg(Country x, Country y) {
	return x.g > y.g;
}
bool cmpj(Country x, Country y) {
	return x.j > y.j;
}
bool cmpgp(Country x, Country y) {
	return x.g / x.p > y.g / y.p;
}
bool cmpjp(Country x, Country y) {
	return x.j / x.p > y.j / y.p;
}

int main() {
	int n, m;
	int need[s];
	int rank[s][5];
	while (cin >> n >> m) {
		for (int i = 0; i < n; i++) {
			cin >> c[i].g >> c[i].j >> c[i].p;
			c[i].id = i;
		}
		for (int i = 0; i < m; i++) {
			cin >> need[i];
		}

		sort(c, c + n, cmpg);
		rank[c[0].id][1] = 1;
		for (int i = 1; i < n; i++) {
			if (c[i].g == c[i - 1].g)
				rank[c[i].id][1] = rank[c[i - 1].id][1];
			else
				rank[c[i].id][1] = i + 1;
		}

		sort(c, c + n, cmpj);
		rank[c[0].id][2] = 1;
		for (int i = 1; i < n; i++) {
			if (c[i].j == c[i - 1].j)
				rank[c[i].id][2] = rank[c[i - 1].id][2];
			else
				rank[c[i].id][2] = i + 1;
		}

		sort(c, c + n, cmpgp);
		rank[c[0].id][3] = 1;
		for (int i = 1; i < n; i++) {
			if (c[i].g / c[i].p == c[i - 1].g / c[i - 1].p)
				rank[c[i].id][3] = rank[c[i - 1].id][3];
			else
				rank[c[i].id][3] = i + 1;
		}

		sort(c, c + n, cmpjp);
		rank[c[0].id][4] = 1;
		for (int i = 1; i < n; i++) {
			if (c[i].j / c[i].p == c[i - 1].j / c[i - 1].p)
				rank[c[i].id][4] = rank[c[i - 1].id][4];
			else
				rank[c[i].id][4] = i + 1;
		}

		for (int i = 0; i < m; i++) {
			int min = n + 1, type = 5;
			for (int t = 1; t <= 4; t++) {
				int tmp = 1;
				for (int j = 0; j < m; j++) {
					if (i != j) {
						if (rank[need[i]][t] > rank[need[j]][t]) {
							tmp++;
						}
					}
				}
				if (min > tmp) {
					min = tmp;
					type = t;
				}
			}
			cout << min << ":" << type << endl;
		}
		cout << endl;
	}
}
提示

本题需要解决的是奥运会中各国家最有利的排名方式以及名次。只要进行五次排序即可。首先读入各国家信息，写好国家编号，计算和存储排名所需要的数据。然后按四种排名方式分别对需要排名的国家进行排名，并记录名次。最后使用国家编号对国家进行排名。这样就可以输出结果了。


问题 H: 字符串的查找删除

题目描述

给定一个短字符串（不含空格），再给定若干字符串，在这些字符串中删除所含有的短字符串。

输入

输入只有1组数据。
输入一个短字符串（不含空格），再输入若干字符串直到文件结束为止。

输出

删除输入的短字符串(不区分大小写)并去掉空格,输出。

样例输入
1
2
3
4
5
6
7
in
#include 
int main()
{

printf(" Hi ");
}
样例输出
1
2
3
4
5
6
#clude
tma()
{

prtf("Hi");
}
提示

注:将字符串中的In、IN、iN、in删除。

思路

使用了几个函数：

  • tolower()：将字符转换为小写
  • string.find(str,index)：在string里面查找str子串，index指定开始查找的位置，若找到,返回该字串的位置；若未找到，返回string::npos
  • string.erase(index,length)：从index开始删除string中长度为length的子串

知道了上面函数的使用方法后，思路上也就没什么难的了，注意比较前要先都转换为小写（题中不区分大小写）。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <string>
#include <cctype>
using namespace std;
int main()
{
    string del, rep, lrep;
    int index, k;
    getline(cin, del);
    for (int i = 0; i < del.length(); i++)
    {
        del[i] = tolower(del[i]);
    }
    while (getline(cin, rep))
    {
        lrep = "";
        index = 0;
        for (int i = 0; i < rep.length(); i++)
        {
            lrep += tolower(rep[i]);
        }
        while (lrep.find(del, index) != string::npos)
        {
            k = lrep.find(del, index);
            lrep.erase(k, del.length());
            rep.erase(k, del.length());
            index = k;
        }
        index = 0;
        while (lrep.find(" ", index) != string::npos)
        {
            k = lrep.find(" ", index);
            lrep.erase(k, 1);
            rep.erase(k, 1);
            index = k;
        }
        cout << rep << endl;
    }
    return 0;
}

问题 I: 后缀子串排序

题目描述

对于一个字符串，将其后缀子串进行排序，例如grain
其子串有：
grain
rain
ain
in
n
然后对各子串按字典顺序排序，即：
ain,grain,in,n,rain

输入

每个案例为一行字符串。

输出

将子串排序输出

样例输入
1
2
grain
banana
样例输出
1
2
3
4
5
6
7
8
9
10
11
ain
grain
in
n
rain
a
ana
anana
banana
na
nana
思路

双重循环，外层循环遍历字符串中每一个字符作为当前子串的首字符，内层循环从该首字符一直取到字符串结束，将所有的子串存到数组里，最后用sort()排序后输出即得到字典序。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
bool cmp(string a, string b)
{
	return a < b;
}

int main()
{
	string str;
	int len;
	while (cin >> str)
	{
		len = str.length();
		string *s = new string[len];
		for (int i = 0; i < len; i++)
		{	
			string temp = "";
			for (int j = i; j < len; j++)
				temp += str[j];
			s[i] = temp;
		}
		sort(s, s+len, cmp);
		for (int i = 0; i < len; i++)
		{
			cout << s[i] << endl;
		}
	}
	return 0;
}

问题 J: 算法10-6~10-8：快速排序

题目描述

快速排序是对起泡排序的一种改进。它的基本思想是，通过一趟排序将待排序的记录分割成两个独立的部分，其中一部分记录的关键字均比另一部分的关键字小，在分成两个部分之后则可以分别对这两个部分继续进行排序，从而使整个序列有序。
快速排序的算法可以描述如下：
在这里插入图片描述

在本题中，读入一串整数，将其使用以上描述的快速排序的方法从小到大排序，并输出。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过100000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入
1
2
10
2 8 4 6 1 10 7 3 5 9
样例输出
1
1 2 3 4 5 6 7 8 9 10
提示

在本题中，需要按照题目描述中的算法完成快速排序的算法。

快速排序是一种十分常用的排序算法，其平均时间复杂度为O(knlnn)，其中n为待排序序列中记录的个数，k为常数。大量的实际应用证明，在所有同数量级的此类排序算法中，快速排序的常数因子k是最小的，因此，就平均时间而言，快速排序是目前被认为最好的一种内部排序方法。

而在C语言的常用编译器中，qsort函数是一个非常常用的快速排序函数。

思路

考试应该不会出这么耿直的题，直接sort()就好了…

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<iostream>
using namespace std;
int Partition(int a[], int low, int high)
{
	int loc = low;
	int key = a[low];
	for (int i = low + 1; i <= high; i++)
	{
		if (a[i] < key)
		{
			loc++;
			if (loc != i)
			{
				int temp = a[i];
				a[i] = a[loc];
				a[loc] = temp;
			}
		}
	}
	a[low] = a[loc];
	a[loc] = key;
	return loc;
}
void Qsort(int a[], int low, int high)
{
	if (low < high)
	{
		int loc = Partition(a, low, high);
		Qsort(a, low, loc - 1);
		Qsort(a, loc + 1, high);
	}
}
int main()
{
	int n;
	cin >> n;
	int *a = new int[n];
	for (int i = 0; i < n; i++)
		cin >> a[i];
	Qsort(a, 0, n - 1);
	for (int i = 0; i < n; i++)
		cout << a[i] << " ";
	cout << endl;
	system("pause");
	return 0;
}

问题 K: 为什么1024是程序员节

题目描述

小雏鸟正在看剧。突然被插播的广告吓了一跳。

只见广告上说 1024你懂的

小雏鸟不懂， 问身边的大白。大白说，这个1024是2的10次方，程序员把10月24日作为程序猿日。

现在给你一个整数N，让你求2的N次方有多大。

输入

一个整数N，N<30

输出

一个整数，2的N次方的结果

样例输入
1
10
样例输出
1
1024
思路

水题

代码
1
2
3
4
5
6
7
8
9
10
11
12
#include<iostream>
using namespace std;
int main()
{
	int n, res = 1;
	cin >> n;
	//res = pow(2,n);
	for (int i = 0; i < n; i++)
		res *= 2;
	cout << res << endl;
	return 0;
}


实验二

问题 A: 子网掩码

题目描述

子网掩码是用来判断任意两台计算机的IP地址是否属于同一子网络的根据。
最为简单的理解就是两台计算机各自的IP地址与子网掩码进行AND运算后，如果得出的结果是相同的，则说明这两台计算机是处于同一个子网络上的，可以进行直接的通讯。就这么简单。

请看以下示例：

运算演示之一：
IP地址　 192.168.0.1
子网掩码　 255.255.255.0

转化为二进制进行运算：
IP地址　 11010000.10101000.00000000.00000001
子网掩码　11111111.11111111.11111111.00000000

AND运算：
　　　　　11010000.10101000.00000000.00000000

转化为十进制后为：
　　　　　　192.168.0.0

运算演示之二：
IP地址　 192.168.0.254
子网掩码　 255.255.255.0

转化为二进制进行运算：
IP地址　 11010000.10101000.00000000.11111110
子网掩码　11111111.11111111.11111111.00000000

AND运算：
　　　　　11010000.10101000.00000000.00000000

转化为十进制后为：
　　　　　　192.168.0.0

运算演示之三：
IP地址　 192.168.0.4
子网掩码　 255.255.255.0

转化为二进制进行运算：
IP地址　 11010000.10101000.00000000.00000100
子网掩码　11111111.11111111.11111111.00000000

AND运算：
　　　　　11010000.10101000.00000000.00000000

转化为十进制后为：
　　　　　　192.168.0.0

通过以上对三组计算机IP地址与子网掩码的AND运算后，我们可以看到它运算结果是一样的，均为192.168.0.0，所以计算机就会把这三台计算机视为在同一子网络。

输入

···
输入的第一行是本机IP地址；
第二行是子网掩码；
第三行是一个整数N，表示后面有N个IP地址；
接下来N行：
第1个IP地址
…
…
第N个IP地址

输出

计算并输出N个IP地址是否与本机在同一子网内。对于在同一子网的输出“INNER”，对于在不同子网的输出“OUTER”。

样例输入
1
2
3
4
5
6
192.168.0.1
255.255.255.0
3
192.168.0.2
192.168.0.254
192.168.1.2
样例输出
1
2
3
INNER
INNER
OUTER
思路

我的思路是用string类存储ip地址和子网掩码，然后分为四段将string类转换为int型后再进行与运算，最后的结果进行判断。

  • dot2space(string a)将输入中的.替换为空格，方便后续进行分割。
  • clca(string ip,string sub)根据ip地址和子网掩码计算想与后的地址
  • 这里分割成四段以及将string转换为int，均可以用sstrean头文件中的stringstream流来操作。>>会以空格作为分割从stringstream流中提取字符串，在赋给int型数组元素的时候完成转换。

肯定还有其他的思路，我的代码太丑..

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
#include <string>
#include <sstream>
using namespace std;
string dot2space(string a)
{
    for (int i = 0; i < a.length(); i++)
    {
        if (a[i] == '.')
        {
            a[i] = ' ';
        }
    }
}
string clca(string ip, string sub)
{
    int ip2[4], sub2[4];
    string addr = "";
    ip = dot2space(ip);
    sub = dot2space(sub);
    stringstream s1(ip);
    stringstream s2(ip);
    for (int i = 0; i < 4; i++)
    {
        s1 >> ip[i];
        s2 >> sub[i];
        addr += to_string(ip2[i] & sub2[i]);
    }
    return addr;
}
int main()
{
    string localIP, sub, addr;
    int n;
    cin >> localIP >> sub;
    cin >> n;
    addr = clca(localIP, sub);
    string *ip = new string[n];
    for (int i = 0; i < n; i++)
    {
        cin >> ip[i];
    }
    for (int i = 0; i < n; i++)
    {
        if (clca(ip[i], sub) == addr)
            cout << "INNER" << endl;
        else
            cout << "OUTER" << endl;
    }
    return 0;
}

问题 B: 快来秒杀我

题目描述

根据前几次竞赛的情况，这次为了给新手们一点信心，特提供这道秒杀题来让大家杀。
ASCII码大家应该都学过了，现在给你一个很简单的任务，输入数字，表示ASCII码，输出对应的文本内容。

输入

输入的第一行是一个整数T（1<=T<=100）。
接下来输入T个正整数，这些数之间用空格、换行或Tab键来分隔。
测试数据保证输入的整数都在ASCII码范围内，并且不小于32。

输出

在一行中输出对应的文本内容。

样例输入
1
2
3
13
72 101 108 108 111 44
32 119 111 114 108 100 33
样例输出
1
Hello, world!
思路

水题，没啥好说的，强制类型转换一下即可。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<iostream>
using namespace std;
const int maxn = 105;
int a[maxn], t;
int main()
{
    cin >> t;
    for (int i = 0; i < t;i++)
    {
        cin >> a[i];
    }
    for (int i = 0; i < t;i++)
    {
        cout << (char)a[i];
    }
    return 0;
}

问题 C: 最短路径1

题目描述

有n个城市m条道路（n<1000, m<10000)，每条道路有个长度，请找到从起点s到终点t的最短距离和经过的城市名。

输入

输入包含多组测试数据。

每组第一行输入四个数，分别为n，m，s，t。

接下来m行，每行三个数，分别为两个城市名和距离。

输出

每组输出占两行。

第一行输出起点到终点的最短距离。

第二行输出最短路径上经过的城市名，如果有多条最短路径，输出字典序最小的那条。若不存在从起点到终点的路径，则输出“can’t arrive”。

样例输入
1
2
3
4
3 3 1 3
1 3 3
1 2 1
2 3 1
样例输出
1
2
2
1 2 3
思路

当时OJ可能有些问题，所有人都超时，所以就没认真写… 现在重新写了一下，测试了几组数据没问题，但没经过OJ的检验。

用的是Dijkstra算法：

  • dist数组存每个点距离起始点的距离；
  • book数组存放已经确定最短路径的点；
  • 二维数组e[i][j]存放i到j的距离，距离为inf时表示不可达；
  • pre数组存放最优解中终点的前一个要经过的点（如果不需要输出路径，只要输出最后的路径长度，则不需要这个数组）

然后就和书上的思路一样了，不断更新dist、book、pre三个数组，最后用pre数组递归输出路径，例如：若1->5的最短路径前面一个经过的点为4（即路径为1->...->4->5），那么就去递归查询1->4的最短路径；若1->4的最短路径前面一个经过的点为3（即路径为1->...->3->4->5），那么就递归查询1->3的最短路径……直到起始点。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include <iostream>
using namespace std;
const int maxn = 1005;
int n, m, s, t;
int inf = 0xffffff;
int book[maxn], dist[maxn], pre[maxn];
int e[maxn][maxn];
void TraceBack(int pre[], int n)
{
    if (n == s)
    {
        cout << n << " ";
    }
    else
    {
        TraceBack(pre, pre[n]);	//递归输出点n前一个点的最短路径
        cout << n << " ";		//输出点n
    }
}
int main()
{
    //n个顶点，m条边
    cin >> n >> m >> s >> t;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            if (i == j)
            {
                e[i][j] = 1;
            }
            else
            {
                e[i][j] = inf;
            }
        }
    }
    //读入初始边
    while (m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        e[a][b] = c; //a->b 距离为c
    }
    //初始化dis数组和pre数组
    for (int i = 1; i <= n; i++)
    {
        dist[i] = e[s][i];
        if (dist[i] != inf)
        {
            pre[i] = s;
        }
    }
    //设起点前面的点为0
    pre[s] = 0;
    //初始化book数组
    for (int i = 1; i <= n; i++)
    {
        book[i] = 0;
    }
    //将起点加入S集合中
    book[s] = 1;

    //Dijkstra
    for (int i = 1; i <= n; i++)
    {
        int u, min = inf;
        for (int j = 1; j <= n; j++)
        {
            if (book[j] == 0 && dist[j] < min)
            {
                min = dist[j];
                u = j;
            }
        }
        book[u] = 1;
        for (int k = 1; k <= n; k++)
        {
            if (e[u][k] < inf)
            {
                if (dist[k] > dist[u] + e[u][k])
                {
                    dist[k] = dist[u] + e[u][k];
                    pre[k] = u;
                }
            }
        }
    }
    if (dist[t] < inf)
    {
        cout << dist[t] << endl;
        TraceBack(pre, t);
    }
    else
    {
        cout << "can't arrive" << endl;
    }
    return 0;
}


问题 D: 二叉排序树

题目描述

输入一系列整数，建立二叉排序数，并进行前序，中序，后序遍历。

输入

输入第一行包括一个整数n(1<=n<=100)。接下来的一行包括n个整数。

输出

可能有多组测试数据，对于每组数据，将题目所给数据建立一个二叉排序树，并对二叉排序树进行前序、中序和后序遍历。每种遍历结果输出一行。每行最后一个数据之后有一个空格。

样例输入
1
2
3
4
5
6
1
2 
2
8 15 
4
21 10 5 39
样例输出
1
2
3
4
5
6
7
8
9
2 
2 
2 
8 15 
8 15 
15 8 
21 10 5 39 
5 10 21 39 
5 10 39 21
思路

二叉排序树，以递归插入的方式建立二叉树，插入的时候判断与父节点的大小，小的放左儿子，大的放右儿子。

前序、中序、后序遍历就不说了换一下位置就好了。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>
using namespace std;
struct node
{
    int data;
    node *lchild;
    node *rchild;
    node(int num) : data(num), lchild(NULL), rchild(NULL) {}
};
void insert(int num, node *&T) //*&是关键
{
    if (!T)
    {
        T = new node(num);
    }
    else if (num < T->data)
    {
        insert(num, T->lchild);
    }
    else if (num > T->data)
    {
        insert(num, T->rchild);
    }
    return;
}
void preOrder(node *T)
{
    if (!T)
    {
        return;
    }
    cout << T->data << " ";
    preOrder(T->lchild);
    preOrder(T->rchild);
}
void inOrder(node *T)
{
    if (!T)
    {
        return;
    }
    inOrder(T->lchild);
    cout << T->data << " ";
    inOrder(T->rchild);
}

void postOrder(node *T)
{
    if (!T)
    {
        return;
    }
    postOrder(T->lchild);
    postOrder(T->rchild);
    cout << T->data << " ";
}
int main()
{
    int n;
    node *root;
    while (cin >> n)
    {
        int num;
        root = NULL;
        for (int i = 0; i < n; i++)
        {
            cin >> num;
            //以插入的方式建立二叉树
            insert(num, root);
        }
        preOrder(root);
        cout << endl;
        inOrder(root);
        cout << endl;
        postOrder(root);
        cout << endl;
    }
    return 0;
}

问题 E: 密码锁

题目描述

玛雅人有一种密码，如果字符串中出现连续的2012四个数字就能解开密码。给一个长度为N的字符串，（2=<N<=13）该字符串中只含有0,1,2三种数字，问这个字符串要移位几次才能解开密码，每次只能移动相邻的两个数字。例如02120经过一次移位，可以得到20120,01220,02210,02102，其中20120符合要求，因此输出为1.如果无论移位多少次都解不开密码，输出-1。

输入

第一行输入N，第二行输入N个数字，只包含0，1，2

输出
样例输入
1
2
3
4
5
02120
5
02120
样例输出
1
2
1
1
思路

BFS，具体步骤在注释里写的很清楚了….

STL是真的好用

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <string>
#include <queue>
#include <map>
using namespace std;
map<string, int> M;
queue<string> Q;
//交换str的第i位和第i+1位
string Swap(string str, int i)
{
    string newStr = str;
    char tmp = newStr[i];
    newStr[i] = newStr[i + 1];
    newStr[i + 1] = tmp;
    return newStr;
}
//判断是否满足条件
bool Judge(string str)
{
    if (str.find("2012", 0) == string::npos)
        return false;
    else
        return true;
}
//BFS
int BFS(string str)
{
    string newStr;
    M.clear();
    while (!Q.empty())
        Q.pop();
    //初始str入列
    Q.push(str);
    //字符串为键，交换次数为值，初始移动次数为0
    M[str] = 0;
    //只要队列中还有组合的字符串
    while (!Q.empty())
    {
        //队首的字符串出列
        str = Q.front();
        Q.pop();
        //遍历该字符串所有交换2位的组合
        for (int i = 0; i <= str.length() - 1; i++)
        {
            newStr = Swap(str, i);
            //若交换后的新字符串未出现过
            if (M.find(newStr) == M.end())
            {
                //此新字符串的交换次数等于上一轮循环字符串的交换次数加1
                M[newStr] = M[str] + 1;
                //判断该字符是否符合要求，符合则返回交换次数，不符合则将该字符串入列，进行下一轮遍历
                if (Judge(newStr))
                    return M[newStr];
                else
                    Q.push(newStr);
            }
            //如果该新字符串已出现过，则直接跳过
            else
                continue;
        }
    }
    return -1;
}
int main()
{
    int n;
    string str;
    while (cin >> n)
    {
        cin >> str;
        if (Judge(str) == true)
            cout << "0" << endl;
        else
        {
            int ans = BFS(str);
            cout << ans << endl;
        }
    }
    return 0;
}


问题 F: 算法10-6~10-8：快速排序

题目描述

快速排序是对起泡排序的一种改进。它的基本思想是，通过一趟排序将待排序的记录分割成两个独立的部分，其中一部分记录的关键字均比另一部分的关键字小，在分成两个部分之后则可以分别对这两个部分继续进行排序，从而使整个序列有序。
快速排序的算法可以描述如下：
在这里插入图片描述
在本题中，读入一串整数，将其使用以上描述的快速排序的方法从小到大排序，并输出。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过100000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入
1
2
10
2 8 4 6 1 10 7 3 5 9
样例输出
1
1 2 3 4 5 6 7 8 9 10
提示

在本题中，需要按照题目描述中的算法完成快速排序的算法。

快速排序是一种十分常用的排序算法，其平均时间复杂度为O(knlnn)，其中n为待排序序列中记录的个数，k为常数。大量的实际应用证明，在所有同数量级的此类排序算法中，快速排序的常数因子k是最小的，因此，就平均时间而言，快速排序是目前被认为最好的一种内部排序方法。

而在C语言的常用编译器中，qsort函数是一个非常常用的快速排序函数。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
using namespace std;
int Partition(int a[], int low, int high);
void Qsort(int a[], int low, int high);
int main()
{
	int n;
	cin >> n;
	int *digit = new int[n];
	for (int i = 0; i < n; i++)
		cin >> digit[i];
	Qsort(digit, 0, n-1);
	for (int i = 0; i < n; i++)
		cout << digit[i] << " ";
	cout << endl;
	return 0;
}
int Partition(int a[], int low, int high)
{
	int loc = low;
	int key = a[low];
	for (int i = low + 1; i <= high; i++)
	{
		if (a[i] < key)
		{
			loc++;
			if (i != loc)
			{
				int temp = a[i];
				a[i] = a[loc];
				a[loc] = temp;
			}
		}
	}
	a[low] = a[loc];
	a[loc] = key;
	return loc;
}
void Qsort(int a[], int low, int high)
{
	if (low < high)
	{
		int loc = Partition(a, low, high);
		Qsort(a, low, loc - 1);
		Qsort(a, loc + 1, high);
	}
}

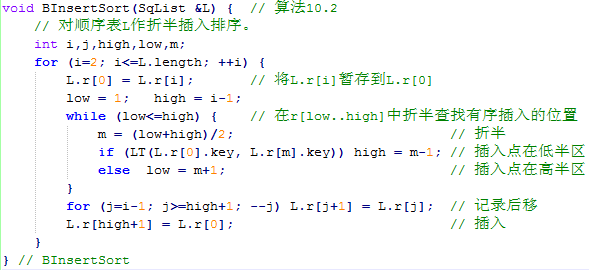
问题 G: 算法10-2：折半插入排序

题目描述

折半插入排序同样是一种非常简单的排序方法，它的基本操作是在一个已经排好序的有序表中进行查找和插入。不难发现这个查找的过程可以十分自然的修改成折半查找的方式进行实现。
折半插入排序的算法可以描述如下：
在这里插入图片描述
在本题中，读入一串整数，将其使用以上描述的折半插入排序的方法从小到大排序，并输出。

输入

输入的第一行包含1个正整数n，表示共有n个整数需要参与排序。其中n不超过1000。
第二行包含n个用空格隔开的正整数，表示n个需要排序的整数。

输出

只有1行，包含n个整数，表示从小到大排序完毕的所有整数。
请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入
1
2
10
2 8 4 6 1 10 7 3 5 9
样例输出
1
1 2 3 4 5 6 7 8 9 10
提示

在本题中，需要按照题目描述中的算法完成折半插入排序的算法。与直接插入排序算法不同，折半插入排序算法在查找插入位置时采用了折半查找的方案，减少了关键字之间的比较次数，但是记录的移动次数并没有发生改变，因此折半插入排序的时间复杂度依旧为O(n2)，同样不是一种非常高效的排序方法。

思路

折半插入排序，即假设前面序列已经是有序的情况下，将下一个数利用二分法查找出在前面有序序列中的位置，然后将其插入进去，知道全部序列有序。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
using namespace std;
void BInsertSort(int data[], int left, int right)
{
	int temp, low, high, mid;
	for (int i = left + 1; i <= right; i++)
	{
		temp = data[i];
		low = left;
		high = i - 1;
		while (low <= high)
		{
			mid = (low + high) / 2;
			if (temp < data[mid])
				high = mid - 1;
			else
				low = mid + 1;
		}
		for (int j = i - 1; j >= low; j--)
			data[j + 1] = data[j];
		data[low] = temp;
	}
}
int main()
{
	int n;
	cin >> n;
	int *digit = new int[n];
	for (int i = 0; i < n; i++)
		cin >> digit[i];
	BInsertSort(digit, 0, n - 1);
	for (int i = 0; i < n; i++)
		cout << digit[i] << " ";
	cout << endl;
	return 0;
}

问题 H: 算法7-9：最小生成树

题目描述

最小生成树问题是实际生产生活中十分重要的一类问题。假设需要在n个城市之间建立通信联络网，则连通n个城市只需要n-1条线路。这时，自然需要考虑这样一个问题，即如何在最节省经费的前提下建立这个通信网。
可以用连通网来表示n个城市以及n个城市之间可能设置的通信线路，其中网的顶点表示城市，边表示两个城市之间的线路，赋于边的权值表示相应的代价。对于n个顶点的连通网可以建立许多不同的生成树，每一棵生成树都可以是一个通信网。现在，需要选择一棵生成树，使总的耗费最小。这个问题就是构造连通网的最小代价生成树，简称最小生成树。一棵生成树的代价就是树上各边的代价之和。
而在常用的最小生成树构造算法中，普里姆（Prim）算法是一种非常常用的算法。以下是其算法的大致结构：
在这里插入图片描述
在本题中，读入一个无向图的邻接矩阵（即数组表示），建立无向图并按照以上描述中的算法建立最小生成树，并输出最小生成树的代价。

输入

输入的第一行包含一个正整数n，表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数，对于第i行的第j个整数，如果不为0，则表示第i个顶点和第j个顶点有直接连接且代价为相应的值，0表示没有直接连接。当i和j相等的时候，保证对应的整数为0。
输入保证邻接矩阵为对称矩阵，即输入的图一定是无向图，且保证图中只有一个连通分量。

输出

只有一个整数，即最小生成树的总代价。请注意行尾输出换行。

样例输入
1
2
3
4
5
4
0 2 4 0
2 0 3 5
4 3 0 1
0 5 1 0
样例输出
1
6
提示

在本题中，需要掌握图的深度优先遍历的方法，并需要掌握无向图的连通性问题的本质。通过求出无向图的连通分量和对应的生成树，应该能够对图的连通性建立更加直观和清晰的概念

思路

用的是Prim算法，实现起来和最小路径的步骤差不多，同样是二维数组存两个点之间的距离，inf表示不可达；book数组存放已经加到最小生成树里的点 。

区别在于这里的dist数组存放的是每个点距离最小生成树的最短距离（注意不是起始点，或者说根节点），这样每次更新dist数组的时候只需要比较dist[j]和e[u][j]的大小，而不用加上dist[u]了。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <iostream>
using namespace std;
int inf = 0xffffff;
int main()
{
    int n, dist[55], book[55], e[55][55];
    while (cin >> n)
    {
        int sum = 0, count = 0;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                cin >> e[i][j];
                if (i != j && e[i][j] == 0)
                {
                    e[i][j] = inf;
                }
            }
        }
        //初始化dist数组和book数组
        for (int i = 1; i <= n; i++)
        {
            dist[i] = e[1][i];
            book[i] = 0;
        }
        //将1号加到生成树中，并将count加一
        book[1] = 1;
        count++;
        //最小生成树总共加入n-1个结点即可
        while (count < n)
        {
            int min = inf, u;
            //找出距离二叉树最小的点
            for (int i = 1; i <= n; i++)
            {
                if (book[i] == 0 && dist[i] < min)
                {
                    min = dist[i];
                    u = i;
                }
            }
            //将该点假如到生成树中,同时count加1
            book[u] = 1;
            count++;
            //加上生成树到该点的边的权值
            sum += dist[u];
            //更新dist
            for (int j = 1; j <= n; j++)
            {
                //找不在生成树中，且距离生成树的距离大于更新后的点
                if (book[j] == 0 && dist[j] > e[u][j])
                {
                    dist[j] = e[u][j];
                }
            }
        }
        cout << sum << endl;
    }
    return 0;
}

问题 J: 奶牛的聚会

题目描述

农历新年马上就要到了，奶牛们计划举办一次聚会庆祝新年的到来。但是，奶牛们并不喜欢走太远的路，这会给他们的聚会带来消极情绪，当一头奶牛的消极指数为Wi，他参加聚会所需行走的距离为si，那么他就会给聚会带来Si3*Wi的消极情绪。所有奶牛所在位置都在一条直线上，已知所有奶牛的坐标和消极指数，求如何确定聚会地点，使得所有奶牛给聚会带来的消极情绪之和最小，输出消极情绪之和的最小值。

输入

第一行包含一个整数 Ca(Ca<=20) ，表示有 Ca 组测试数据。

对于每组测试数据：第一行包含一个整数n(1<=n<=50000) ，表示奶牛的数量。接下来 n 行每行包含两个浮点数Si和wi (-106<=Si<=106, 0<Wi<15)。

输出

对于每组测试数据，输出 “Case #c: ans” ，其中c表示测试数据编号，ans表示消极情绪之和的最小值，结果四舍五入为一个整数。

样例输入
1
2
3
4
5
6
7
1
5
0.9 2
1.4 4
3.1 1
6.2 1
8.3 2
样例输出
1
Case #1: 300
思路

三分查找法确定消极情绪之和最小的位置，结合注释应该不难理解。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <math.h>
using namespace std;
typedef long long ll;
const int maxn = 50010;
double Si[maxn], wi[maxn];
int n, Ca;
//计算聚会位置在pos时的消极情绪之和
double ans(double pos)
{
    double sum = 0;
    for (int i = 0; i < n; i++)
    {
        //计算每个奶牛距离聚会位置的距离(非负)
        double dist = Si[i] - pos;
        if (dist < 0)
            dist = -dist;
        sum += pow(dist, 3) * wi[i];
    }
    return sum;
}
int main()
{
    cin >> Ca;
    for (int i = 1; i <= Ca; i++)
    {
        cin >> n;
        for (int j = 0; j < n; j++)
        {
            cin >> Si[j] >> wi[j];
        }
        //找到坐标位置最小的奶牛
        double low = Si[0];
        for (int k = 0; k < n; k++)
            if (Si[k] < low)
                low = Si[k];
        //找到坐标位置最小的奶牛
        double high = Si[0];
        for (int l = 0; l < n; l++)
            if (Si[l] > high)
                high = Si[l];
        //三分查找法确定最终位置
        while (high - low > 1e-7)
        {
            double m1 = (high + low) / 2.0;
            double m2 = (m1 + high) / 2.0;
            if (ans(m1) > ans(m2))
                low = m1;
            else
                high = m2;
        }
        cout << "Case #" << i << ": " << ll(ans(low) + 0.5) << endl;
    }
    return 0;
}