递归与分支
内部收益率
题目描述

输入

输出
对于每组数据,输出仅一行,即项目的IRR,四舍五入保留小数点后两位。
样例输入
1 | 1 |
样例输出
1 | 1.00 |
代码
1 |
|
问题 J: 奶牛的聚会
题目描述
农历新年马上就要到了,奶牛们计划举办一次聚会庆祝新年的到来。但是,奶牛们并不喜欢走太远的路,这会给他们的聚会带来消极情绪,当一头奶牛的消极指数为Wi,他参加聚会所需行走的距离为si,那么他就会给聚会带来Si3*Wi的消极情绪。所有奶牛所在位置都在一条直线上,已知所有奶牛的坐标和消极指数,求如何确定聚会地点,使得所有奶牛给聚会带来的消极情绪之和最小,输出消极情绪之和的最小值。
输入
第一行包含一个整数 Ca(Ca<=20) ,表示有 Ca 组测试数据。
对于每组测试数据:第一行包含一个整数n(1<=n<=50000) ,表示奶牛的数量。接下来 n 行每行包含两个浮点数Si和wi (-106<=Si<=106, 0<Wi<15)。
输出
对于每组测试数据,输出 “Case #c: ans” ,其中c表示测试数据编号,ans表示消极情绪之和的最小值,结果四舍五入为一个整数。
样例输入
1 | 1 |
样例输出
1 | Case #1: 300 |
思路
三分查找法确定消极情绪之和最小的位置,结合注释应该不难理解。
代码
1 |
|
问题 E: 光合作用
题目描述
蒜头是个爱学习的孩子,他总喜欢在生活中做一些小实验,这次蒜头想研究一下光合作用。蒜头的实验材料有如下几样:神奇的种子,普通的纸箱和一些光源。一开始,蒜头将种子均匀的种在了箱子底部,你可以将其看成 X 轴,种子的位置为 X 轴上的点。然后蒜头用纸板将箱子盖住,并在纸板上安装了一些光源(具体见图,顶上的为光源,光源两边与顶部的夹角都为45度,黄色部分为光照,绿色的为植物。)。神奇的种子会在有光的情况下一直向上生长直到没光为止。现在蒜头想知道当实验结束时每颗种子的高度是多少?
输入
第一行输入一个整数 T,表示测试数据的组数。
每组数据的第一行是三个整数 n,m,h(1<=n,m<=1e5,0<=m<=1e5,1<=h<=1e4),n表示种子数(编号为1,2…n),m表示光源数,h 表示箱子的高度。
接下来m行,每行一个整数Xi表示第i个光源在顶部的位置。
输出
对于每组测试数据,请输出n行,每行一个数表示第i颗种子的最终高度。
样例输入
1 | 2 |
样例输出
1 | 0 |
思路
二分法
代码
1 |
|
动态规划
跳台阶
题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
输入
多组测试样例。每组测试样例包含一个整数n。(1<=n<=100)
输出
每组测试样例输出一行,表示青蛙跳上n级台阶的跳法数量.
所得到的结果模1000000007
样例输入
1 | 3 |
样例输出
1 | 3 |
思路
可以有多种方法,我这里选用动态规划。
dp[i]表示i阶台阶的跳法有多少种,一次只能跳一阶或两阶。
已知dp[1]=1,dp[2]=2,所以dp[i]=dp[i-1]+dp[i-2],表示:
到达i阶 = (最后一步跳一阶到达i)+ (最后一步跳两阶到达i)
代码
1 |
|
最长公共子序列
题目描述
给你一个序列X和另一个序列Z,当Z中的所有元素都在X中存在,并且在X中的下标顺序是严格递增的,那么就把Z叫做X的子序列。
例如:Z=<a,b,f,c>是序列X=<a,b,c,f,b,c>的一个子序列,Z中的元素在X中的下标序列为<1,2,4,6>。
现给你两个序列X和Y,请问它们的最长公共子序列的长度是多少?
输入
输入包含多组测试数据。每组输入占一行,为两个字符串,由若干个空格分隔。每个字符串的长度不超过100。
输出
对于每组输入,输出两个字符串的最长公共子序列的长度。
样例输入
1 | abcfbc abfcab |
样例输出
1 | 4 |
思路


代码
1 |
|
矩阵连乘
题目描述
给定n个矩阵{A1,A2,…,An},及m个矩阵连乘的表达式,判断每个矩阵连乘表达式是否满足矩阵乘法法则,如果满足,则计算矩阵的最小连乘次数,如果不满足输出“MengMengDa“。
输入
输入数据由多组数据组成(不超过10组样例)。每组数据格式如下:
第一行是2个整数n (1≤n≤26)和m(1≤m≤3),表示矩阵的个数。
接下来n行,每行有一个大写字母,表示矩阵的名字,后面有两个整数r和c,分别表示该矩阵的行数和列数,其中1<r, c<100。
第n+1行到第n+m行,每行是一个矩阵连乘的表达式(2<=矩阵个数<=100)。
输出
对于每个矩阵连乘表达式,如果运算不满足矩阵乘法法则的情况(即左矩阵列数与右矩阵的行数不同),则输出“MengMengDa”,否则输出最小矩阵连乘次数。
数据保证结果不超过1e9。
样例输入
1 | 3 2 |
样例输出
1 | 7500 |
思路
矩阵连乘递归式: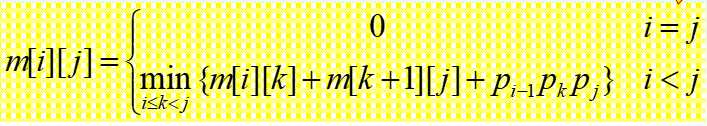
矩阵连乘的部分不是很复杂,一个函数即可完成,主要的代码量集中在数据的输入和转换上。
- 用结构体Matrix表示矩阵的行和列
- 再map存储名字和对应的矩阵
- 将输入的矩阵转换为p数组的同时,判断每相邻的两个矩阵,前一矩阵的行数是否等于后一矩阵的列数,若存在不等的情况,直接输出
MengMengda;否则将其列数存入p数组内
代码
1 |
|
01背包问题
题目描述
已知有N种物品和一个可容纳C重量的背包。每种物品i的重量为Wi,价值为Pi。那么,采用怎样的装包方法才会使装入背包物品的总价值最大。
输入
包含多组测试数据。第一行为一个整数T(1<=T<=10),代表测试数据个数。
接下来有T组测试数据。每组测试数据第一行为背包的重量C(C<10000)和物品个数N(N<1000)。接下来的N行分别为物品的重量cost(1<=cost<=100)和价值val(1<=val<=3000000)。(注意:结果可能超过int范围)
输出
对每组测试数据,输出其对应的所装物品的最大价值。
样例输入
1 | 1 |
样例输出
1 | 15 |
思路
m(i,j)表示背包容量为j,可选物品为i,i+1,...,n时的最优解。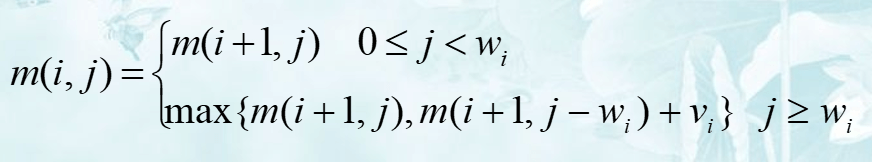
这一题不知道为什么用cin\cout就会报错,用scanf和printf则正确…
代码
1 |
|
最大子段和
题目描述
给定n个整数组成的序列a1,a2,…an, 求子段和ai+ai+1+…+aj(子段可为空集)的最大值。
输入
包含多组测试数据。第一行为一个整数T(1<=T<=20),代表测试数据个数。
每组测试数据第一行为一个整数n,代表有n个整数(1<=n<=10000)。
接下来一行有n个数x(-1000<=x<=1000)。
输出
输出其对应的最大子段和。
样例输入
1 | 1 |
样例输出
1 | 18 |
提示
子段可为空集,答案为0
思路

递归方程如下,b[j]表示1到j的最大字段和: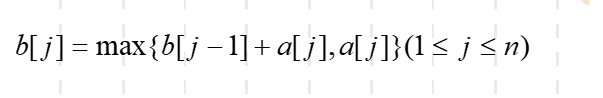
代码
1 |
|
节食的限制
题目描述
Bessie像她的诸多姊妹一样,因為从Farmer John的草地吃了太多美味的草而长出了太多的赘肉。所以FJ将她置於一个及其严格的节食计划之中。她每天不能吃多过H(5<=H<=45000)公斤的乾草。Bessie只能吃一整綑乾草;当她开始吃一綑乾草的之后就再也停不下来了。她有一个完整的N(1<=n<=50)綑可以给她当作晚餐的乾草的清单。她自然想要尽量吃到更多的乾草。很自然地,每綑乾草只能被吃一次(即使在列表中相同的重量可能出现2次,但是这表示的是两綑乾草,其中每綑乾草最多只能被吃掉一次)。 给定一个列表表示每綑乾草的重量Si(1<=Si<=H),求Bessie不超过节食的限制的前提下可以吃掉多少乾草(注意一旦她开始吃一綑乾草就会把那一綑乾草全部吃完)。
输入
第一行:两个由空格隔开的整数:H和N, 第2到N+1行:第i+1行是一个单独的整数,表示第i綑乾草的重量Si。
输出
一个单独的整数表示Bessie在限制范围内最多可以吃多少公斤的乾草。
样例输入
1 | 56 4 |
样例输出
1 | 56 |
思路
重量和价值相等的0-1背包问题。
代码
1 |
|
汽车费用
题目描述
一个特别的单行街道在每公里处有一个汽车站。顾客根据他们乘坐汽车的公里使来付费。例如下表就是一个费用的单子。没有一辆车子行驶超过10公里,一个顾客打算行驶n公里(1<=n<100),它可以通过无限次的换车来完成旅程。最后要求费用最少。
输入
第一行十个整数分别表示行走1到10公里的费用(<=500)。注意这些数并无实际的经济意义,即行驶10公里费用可能比行驶一公里少。第二行一个整数n表示,旅客的总路程数。
输出
仅一个整数表示最少费用。
样例输入
1 | 12 21 31 40 49 58 69 79 90 101 |
样例输出
1 | 147 |
思路
动态规划,依次计算出行走i公里需要的最少费用。
计算行走i公里最少费用时,用j遍历[1~i-1],依次比较price[i]和price[j]+price[i-j]的值,遍历完成后,price[i]为最少费用。
例如,price[4] = min(price[4], price[1]+price[3], price[2]+price[2], price[3]+price[1])
代码
1 |
|
求数组的最长递减子序列
题目描述
给定一个整数序列,输出它的最长递减(注意不是“不递增”)子序列。
输入
输入包括两行,第一行包括一个正整数N(N<=1000),表示输入的整数序列的长度。第二行包括用空格分隔开的N个整数,整数范围区间为[-30000,30000]。
输出
输出最长递减子序列,数字之间有一个空格。
样例输入
1 | 8 |
样例输出
1 | 9 5 4 3 2 |
思路
dp[i]存储[i~n]区间的最长递减子序列,双重循环从后向前遍历,内层循环从[i+1~n],找出最大值小于i的最长递减子序列的长度;外层循环从[n-2~0],将内层循环找到的最大值加一,更新所有的dp[i]。
输出最优解时,因为刚才是从后向前遍历的,所以所有最大递增子序列均在maxpos之后。遍历[maxpos~n],寻找最大递减子序列的下一元素时,只需要判断其值是否小于上一元素且它的最大递减子序列是否比上一元素的小1,即可。
解答
1 |
|
贪心
问题 B: 哈夫曼编码
题目描述
给定一只含有小写字母的字符串;输出其哈夫曼编码的长度
输入
第一行一个整数T,代表样例的个数,接下来T行,每行一个字符串,0<T<=2000,字符串长度0<L<=1500.
输出
对于每个字符串,输出其哈夫曼编码长度
样例输入
1 | 3 |
样例输出
1 | 10 |
思路
哈夫曼编码的思路不难,主要讲一下优先级队列的使用。
在STL里有这个priority_queue,实现优先队列的结构,在优先队列中,优先级高的元素先出队列。
模板声明(3个参数):priority_queue<Type, Container, Functional>
- Type 为数据类型
- Container 为保存数据的容器, 必须是用数组实现的容器,比如
vector、deque但不能用list。默认用的是vector - Functional 为元素比较方式,默认用
operator<, 即队头元素最大。
所以如果后面俩个参数缺省的话,优先队列就是大顶堆,队头元素最大。
如果要用到小顶堆,则一般要把模板的三个参数都带进去。STL里面定义了一个仿函数 greater<>,对于基本类型可以用这个仿函数声明小顶堆priority_queue<int, vector<int>, greater<int> >q;,即队头元素最小。对于自定义类型,则必须自己重载 operator< 或者自己写比较函数。
优先级队列的几个操作:
empty()如果优先队列为空,则返回真pop()删除第一个元素push()插入一个元素size()返回优先队列中拥有的元素的个数top()返回优先队列中有最高优先级的元素解答
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
int main()
{
int T;
cin >> T;
while (T--)
{
char s[1505];
//存放每个字母的频率
int n[26] = {0};
cin >> s;
for (int i = 0; i < strlen(s); i++)
{
n[s[i] - 'a']++;
}
//建立一个优先级队列
priority_queue<int, vector<int>, greater<int>> q;
for (int i = 0; i < 26; i++)
{
if (n[i] > 0)
q.push(n[i]);
}
int sum = 0;
//不断更新优先级队列
while (q.size() >= 2)
{
int a = q.top();
q.pop();
int b = q.top();
q.pop();
int temp = a + b;
q.push(temp);
sum += temp;
}
cout << sum << endl;
}
return 0;
}
问题 D: Homework
题目描述
临近开学了,大家都忙着收拾行李准 备返校,但 I_Love_C 却不为此担心! 因为他的心思全在暑假作业上:目前为止还未开动。
暑假作业是很多张试卷,我们这些从试卷里爬出来的人都知道,卷子上的题目有选择题、填空题、简答题、证明题等。而做选择题的好处就在于工作量很少,但又因为选择题题目都普遍很长。如果有 5 张试卷,其中 4 张是选择题,最后一张是填空题,很明显做最后一张所花的时间要比前 4 张长很多。但如果你只做了选择题,虽然工作量很少,但表面上看起来也已经做了4/5的作业了。
I_Love_C决定就用这样的方法来蒙混过关,他统计出了做完每一张试卷所需的时间以及它做完后能得到的价值(按上面的原理,选择题越多价值当然就越高咯)。
现在就请你帮他安排一下,用他仅剩的一点时间来做最有价值的作业。
输入
测试数据包括多组。每组测试数据以两个整数 M,N(1<M<20,1<N<10000) 开头,分别表示试卷的数目和 I_Love_C 剩下的时间。接下来有 M 行,每行包括两个整数 T,V(1<T<N,1<V<10000)分别表示做完这张试卷所需的时间以及做完后能得到的价值,输入以 0 0 结束。
输出
对应每组测试数据输出 I_Love_C 能获得的最大价值。保留小数点 2 位
提示:float 的精度可能不够,你应该使用 double 类型。
样例输入
1 | 4 20 |
样例输出
1 | 37.00 |
思路
0-1背包类的贪心算法,计算物品性价比,按性价比从大到小排序,优先装入性价比大的,直到容量满为止。
解答
1 |
|
回溯
图的m着色问题
题目描述
给定无向连通图G和m种不同的颜色,用这些颜色给图的各个顶点着一种颜色,若某种方案使得图中每条边的2个顶点的颜色都不相同,则是一个满足的方案,找出所有的方案。
输入
第一行有3个正整数n,k和m,分别表示n个顶点,k条边,m种颜色
接下来k行,每行2个正整数,表示一条边的两个顶点
输出
所有不同的着色方案数
样例输入
1 | 5 8 4 |
样例输出
1 | 48 |
代码
1 |
|
部分和问题
题目描述
给定n个整数,判断是否可以从中选择若干数字,使得他们的和恰好为k。
输入
多组测试用例。
对于每组测试用例,第一行一个正整数n,第二行n个整数,第三行一个整数k。
1≤N≤20,输入整数及k均小于1e8。
输出
若可以使得和为k,输出”Yes”,否则”No”。
样例输入
1 | 4 |
样例输出
1 | Yes |
思路
每个数有加或不加两种可能,可以构造一棵二叉树,深度优先遍历,终止调节为和达到要求(返回true),遍历完全(返回false)。
代码
1 |
|
其他
法师康的工人
题目描述
三个法师康的工人每天早上6点到工厂开始到三条产品生产线上组装桔子手机。第一个工人在200时刻开始(从6点开始计时,以秒作为单位)在生产线上开始生产,一直到1000时刻。第二个工人,在700时刻开始,在1100时刻结束。第三个工人从1500时刻工作到2100时刻。期间最长至少有一个工人在生产线上工作的连续时间为900秒(从200时刻到1100时刻),而最长的无人生产的连续时间(从生产开始到生产结束)为400时刻(1100时刻到1500时刻)。
你的任务是用一个程序衡量N个工人在N条产品线上的工作时间列表(1≤N≤5000,以秒为单位)。
·最长的至少有一个工人在工作的时间段
·最长的无人工作的时间段(从有人工作开始计)
输入
输入第1行为一个整数N,第2-N+1行每行包括两个均小于1000000的非负整数数据,表示其中一个工人的生产开始时间与结束时间。
输出
输出为一行,用空格分隔开两个我们所求的数。
样例输入
1 | 3 |
样例输出
1 | 900 400 |
思路
先按开始时间排序,然后对每个人进行遍历。
如果前人的结束时间小于后人的开始时间,那么中间这段连续时间是没有人的,则更新最长的无人工作的时间。
如果前人的结束时间大于后人的开始时间,就比较两者结束的时间,从前人开始时间到两者间更晚结束的时间内都至少有一个人在,因此更新最长的至少有一个工人在工作的时间。
不断更新直到最后一个人。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
using namespace std;
const int maxn = 5005;
int b[maxn], e[maxn];
struct data
{
int s, e;
} worker[maxn];
bool cmp(struct data a, struct data b)
{
return a.s < b.s;
}
int main()
{
int n, sb, nb;
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> worker[i].s >> worker[i].e;
}
sort(worker, worker + n, cmp);
sb = worker[0].e - worker[0].s;
nb = 0;
int j = 0;
for (int i = 1; i < n; i++)
{
if (worker[i].s <= worker[j].e)
{
worker[j].e = max(worker[i].e, worker[j].e);
sb = max(sb, worker[j].e - worker[j].s);
}
else
{
nb = max(nb, worker[i].s - worker[j].e);
j = i;
}
}
cout << sb << " " << nb << endl;
return 0;
}
配对元素
题目描述
给出2个序列A={a[1],a[2],…,a[n]},B={b[1],b[2],…,b[n]},从A、B中各选出n个元素进行一一配对(可以不按照原来在序列中的顺序),并使得所有配对元素差的绝对值之和最大。
输入
输入的第1行为1个整数n 第2行包含n个整数,题目中的A序列。 第3行包含n个整数,题目中的B序列。
输出
一个数,最大配对
3与6配对,2与7配对,5与4配对,6与1配对,绝对值之差和为14 对于10%的数据,有n≤20; 对于30%的数据,有n≤100; 对于50%的数据,有n≤1000; 对于100%的数据,有n≤10000;a[i],b[i]≤1000。
样例输入
1 | 4 |
样例输出
1 | 14 |
思路
将两个数组分别进行升序和降序排列,然后让一个数组的最大值与另一个数组的最小值相减,依次类推,然后累和即可。
解答
1 |
|
判断日期是否符合格式
题目描述
我们知道一年有12个月,每个月最多有31天,年有平年和闰年之分,本题目要求如果输入一个日期,程序需要判断用户输入的日期是否正确。
提示:测试输入的三个数字中,年份是正数,月份和日期有可能是负数,程序需要对这两个数为负数的情况进行判断。
输入
多组测试用例,对每组测试用例:
用户输入是三个数字,分别表示年,月和日。 例如 2007 10 21 ,表示2007年10月21日,这个输入经过判断是正确的。又例如输入 1993 11 38 ,这个输入经过判断是错误的,因为日期不能超过31天。
输出
程序的输出分为两种,1或者0。1表示输入正确,0表示输入错误。
样例输入
1 | 2011 21 10 |
样例输出
1 | 0 |
思路
闰年判断:(能被4整除&&不能被100整除)||能被400整除
其他没啥好说的,开一个大小为12的数组month[12],存每个月的天数,如果是闰年的话就将month[1]加1
解答
1 |
|
进制转换
题目描述
输入一个十进制正整数,然后输出它所对应的八进制数。
输入
输入一个十进制正整数n(1≤n≤106) 。
输出
输出n对应的八进制数,输出在一行。
样例输入
1 | 10 |
样例输出
1 | 12 |
代码
1 |
|
16级考试题目
问题 A: 星空梦想——鲁班
题目描述
鲁班七号是王者峡谷里的射手,站撸英雄。战场上的鲁班七号,机制强大的鲨嘴炮,立刻将挡在前路的任何物体轰飞。正如他所说的,“借你们的肉体试验下新发明的威力”。是的,这就是鲁班大师和他的天才机关造物鲁班七号。然而,鲁班最为致命的缺点是腿短,跑得慢,一个稍不留神,便会被刺客所击杀。
既然腿短,那么就来多多运动吧,跳跳台阶可还行?假设鲁班七号一次可以跳上1级台阶,但极限一次只能跳上2级台阶(腿短没办法,嘤嘤嘤)。鲁班七号现在从0级阶梯开始,最终跳上第n级的台阶,求总共有多少种跳法?
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=50),代表测试用例个数。
接下来T行,每行输入包含一个整数n(1<=n<=50),代表鲁班最终跳上了第n级台阶。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表鲁班最终跳上第n级台阶的跳法种数。
样例输入
1 | 3 |
样例输出
1 | 3 |
提示
注意结果超过int范围,请用long long类型存储ans
思路
思路一:递归法+打表
思路二:动态规划
用dp[i]表示跳到第i级台阶的方法数,则dp[1]=1、dp[2]=2 … dp[i]=dp[i-1]+dp[i-2],即到第i级台阶的最后一步可以选择跳1级,也可以选择跳2级,而这两种方法的结果我们已经由动态规划得到,直接相加即可。
代码
1 |
|
问题 B: 午夜歌剧——元歌
题目描述
元歌是王者峡谷里的刺客。何谓至高机关之美呢?唯有以至高权力的手令太古奇迹重现人世,方能称得上啊。
是的,元歌擅长操控,所做傀儡能起到以假乱真的作用,今天元歌的傀儡变成你的初中数学老师,给你出个数学题:给你一个数字x,让你求出k7、k6、k5、k4、k3、k2、k1、k0(0<=ki<=9),使得以下等式1成立,最后根据等式2求出最终ans值。
等式1:
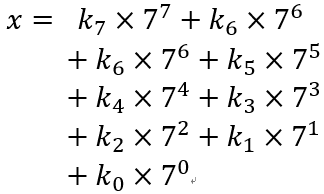
等式2:
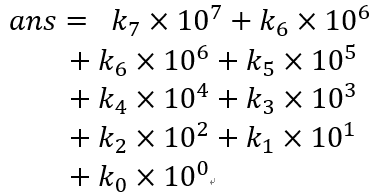
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=1000),代表测试用例个数。
接下来T行,每一行包含一个整数x(1<=x<=1500000)。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表最终运算结果。
样例输入
1 | 3 |
样例输出
1 | 10 |
提示
测试数据均大于等于1,不用特判0
思路
其实就是10进制转7进制
代码
1 |
|
圣诞恋歌——貂蝉
题目描述
貂蝉是王者峡谷里的法师/刺客,貂蝉打法一定要注意配合技能与被动。半肉出装加上蛇皮走位,往往可以1打5,轻松拿下5杀。语花印被动描述为:技能命中会为敌人叠加花之印记,叠加满4层后印记触发被动,会给自身回复生命,同时会对周围敌人造成真实伤害并减速。
我们现在对貂蝉的技能及被动进行简化如下:每使用1次技能会攻击1次目标,每攻击3次目标,会自动额外攻击1次目标。
现在,貂蝉在游戏中使用了n次技能,请问总共会给目标带来多少次攻击。
输入
多组测试数据,第一行输入包含一个整数T,代表测试样例个数。
接下来T行,每行输入包含一个整数n(1<=n<=100),代表貂蝉使用了n次技能。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表貂蝉对目标进行了ans次攻击。
样例输入
1 | 6 |
样例输出
1 | 1 |
提示
没思路,喝瓶汽水冷静下?
思路
每次攻击ans++,攻击次数n--,count来记录攻击的次数,每攻击3次(count==3),则攻击次数加1(白送一次),同时将count清0,知道所剩攻击次数为0,停止。
代码
1 |
|
问题 D: 海之征途——孙策
题目描述
孙策是王者峡谷里的坦克/战士。大船靠岸,江郡欢呼着迎来了他们的新领袖,人称江东小霸王的年轻人。游戏中,孙策的技能长帆破浪,可以驾船冲锋,可将船撞向敌方单位或者阻挡物,并造成一定的伤害。
现在,有一群好奇的江郡小朋友想跟着孙策一起出海航行,但孙策的船承载不了所有小朋友,所以孙策决定,尽可能带更多的小朋友出海,现在请你帮孙策谋一个策略,使得更多的小朋友有机会出海航行。已知的条件是孙策船的最大载重m,以及n个小朋友的体重。
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=1000),代表测试用例个数。
每组测试用例第一行有两个整数m和n。(0<=m<=1000, 0<=n<=1000),分别代表船的载重重量和小朋友的个数,接下来一行为n个小朋友的体重。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表最多能有ans个小朋友跟着一起出海。
样例输入
1 | 2 |
样例输出
1 | 3 |
提示
1.小朋友的体重可能相同 2.船可以满载
思路
贪心算法,先对小朋友按体重升序排列,然后体重小的优先上船,直到容量满为止。
代码
1 |
|
问题 E: 极冰防御——盾山
题目描述
盾山是王者峡谷里的辅助,一夫当关、万夫莫开,一个好的辅助往往可以给团队带来极大帮助。
盾山的游戏中的一个技能为不动如山:手握一块由石头组成的巨盾,张开巨盾砸向地面,将敌人推开,并持续一段时间。
假设盾山最多只能承受C重量的盾牌,而现在有N个小石头,每个石头i的重量为Wi,防御值为Pi。那么,呆萌的盾山想知道,他从N个小石头中挑选M个(M<=N)组成他可承受盾牌,最大的防御值是多少?
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=10),代表测试用例个数。
接下来有T组测试用例。每组测试用例第一行为盾山承受盾牌的最大重量C(C<10000)和小石头的个数N(N<1000)。接下来的N行分别为小石头的重量Wi(1<=Wi<=100)和防御值Pi(1<=Pi<=3000000)。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表可承受盾牌的最大防御值。
样例输入
1 | 1 |
样例输出
1 | 15 |
提示
结果可能超过int范围,请使用long long类型变量
思路
说了这么多,其实就是经典的01背包问题。
之前有一道01背包用cin/cout过不了,只能用scanf/printf,所以到时候看情况吧..
代码
1 |
|