对Deep InfoMax(DIM)的理解

paper: Learning Deep Representations By Mutual Information Estimation and Maximization
arxiv：https://arxiv.org/abs/1808.06670
code：https://github.com/rdevon/DIM
report video：https://www.youtube.com/watch?v=o1HIkn8LEsw&t=256s

1 Introduction

无监督学习一个重要的问题就是学习有用的 representation，本文的目的就是训练一个 representation learning 函数（即编码器encoder） ，其通过最大编码器输入和输出之间的互信息(MI)来学习对下游任务有用的 representation，而互信息可以通过 MINE $^{[1]}$的方法进行估算。

作者还提到，直接最大化全部输入和编码器的输出（即全局的MI）更适合于重建性的任务，而在分类的下游任务上效果不太好。而最大化输入的局部区域（例如不是完整的图片，而是图片中的一块）和输出（即学到的representation）的平均互信息在下游任务（如图像分类）上的效果更好。

因为这种方法类似于对抗自动编码器(AEE, adversarial autoencoders)$^{[2]}$的，将MI最大化和先验匹配结合起来，根据期望的统计特性约束 representation，并且还与 infomax 的优化规则密切相关$^{[3]}$，因此作者称其为 Deep InfoMax(DIM).

因此，文章的主要贡献如下：

• 提出了 Deep InfoMax(DIM)，可以同时估算和最大化输入数据和高级representation之间的互信息(MI)
• 作者提出的最大化互信息的方法，可以根据下游任务是分类还是重建，来对优化全局还是局部的信息进行调整。
• 使用对抗学习约束representation，来使其具有特定于先验的期望统计特征
• 介绍了两种测量 representation 质量的新方法，一个基于Mutual Information Neural Estimation(MINE)$^{[1]}$，一个基于neural dependency measure(NDM)$^{[4]}$，并用它们将DIM与其他无监督学习方法进行比较

2 Objectives of Deep InfoMax

首先，先来看一下传统的图像 encoder 结构 ，如下图：

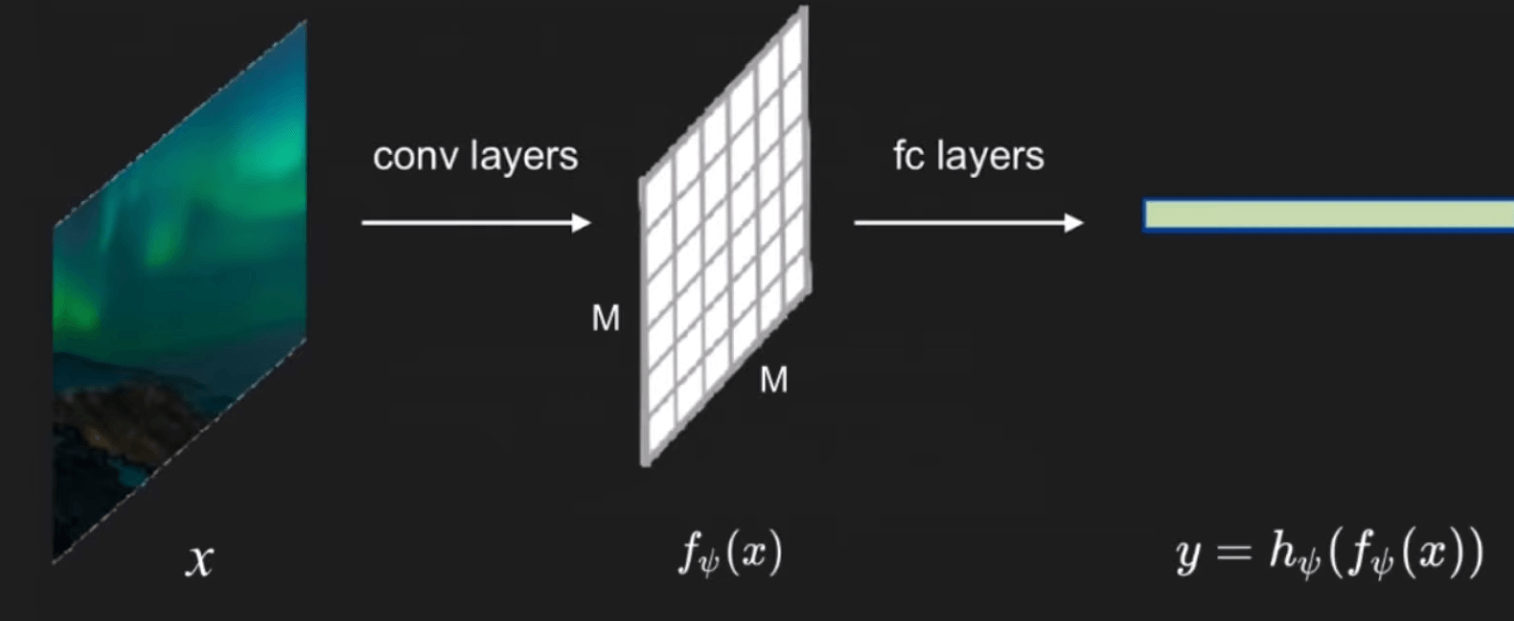
$x$ 表示原始图像，$f_{\psi}(x)$ 表示经过卷积层输出的 $M×M$（注意，DIM 里的 $M×M$ 指的是 $M×M$ 块，而不是像素）的 feature map，而 $y=h_{\psi}\left(f_{\psi}(x)\right)$ 则为经过全连接层之后最终的 feature vector（也可以理解为图像的一种 representation），再将这个 representation 应用于一些下游任务，如分类。

而 DIM 的整体思路如下图，也就是“用图片 encode 后得到的 representation（$y$），与同一张图片的 feature map 组成正样本对，和另一张图片的 feature map 组成负样本对，然后利用 GAN 的思想训练一个 Discriminator 来区分这两中样本对”。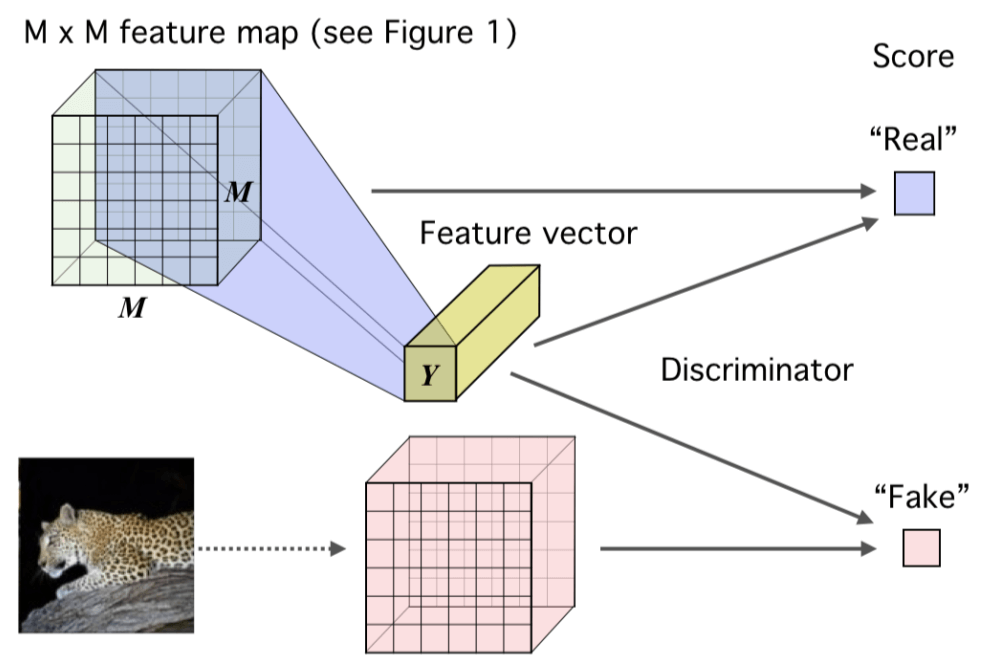

既然要训练 Discriminator ，就不得不提一下 DIM 的损失函数，那么就得先说一下其优化目标。

首先，我们定义一些数学符号：

- $x∈X$为 image 数据集；编码器 encoder 为 ${ E }_{\psi}=h_{\psi} \circ f_{\psi}$ （ $\circ$ 表示是由后面那两个函数组成 ）； $f_{\psi}(x)$ 表示由将原始图像 $x$ 映射到 feature map； $h_{\psi}(f_{\psi}(x))$ 表示将 feature map 再映射到最后的输出 representation，即 $y=h_{\psi}(f_{\psi}(x))=E_{\psi}(x) ∈ Y$。 - 将样本从 $f_{\psi}(X)$ 经过 $h_{\psi}$ 得到的 $y∈Y$ 的分布，也叫做 ”push-forward distribution“（目前还不是很理解这个名词），记作$Q_{\psi,X}$ 而 DIM 最终的优化目标也就是以下两点： - 最大化 $f_{\psi}(X)$ 和 $Y$ 之间的互信息。（作者根据具体任务的不同，又分为了 global 和 local 两种，后面再提） - 在最终的 representation 中再加入一个统计性的约束，使得到的 $y$ 的分布（push-forward distribution）$Q_{\psi,X}$尽量与先验分布 $Q_{prior}$ 相匹配，有点类似对抗自编码器（AAE）。

3 Loss function

Global Infomax

知道了优化目标，下面就是如何去建立和推导该目标的数学表达方式。

我们首先解决第一个优化目标，也就是最大化互信息。互信息就是衡量两个变量的相关性，如果 $X$ 和 $Y$ 相互独立，即$P_{XY}=P_{X}P_{Y}$，那么它们的互信息 $I(X;Y)$ 也就为0。互信息的定义如下：
$$
\begin{aligned}
\mathcal I(X;Y) &=\sum_{X, Y} P(X, Y) \log \frac{P(X \mid Y)}{P(X)} \
\end{aligned} \tag 1
$$
KL散度则是衡量同一个随机变量两个分布之间的差异，其值越小，说明分布越接近，定义如下：
$$
\begin{aligned}
\mathcal D_{KL}(X||Y) &=\mathbb{E}{P{X Y}}[\log \frac{P(X)}{P(Y)}] \
\end{aligned} \tag 2
$$
MI和KL散度之间的关系也不难推导，如下：

$$ \begin{aligned} \mathcal I(X;Y) &=\sum_{X, Y} P(X, Y) \log \frac{P(X \mid Y)}{P(X)} \\ &=\iint P(X,Y)log \frac{P(X|Y)}{P(X)} \\ &=\mathbb{E}_{P_{X Y}}[log \frac{P(X|Y)}{P(X)}] \\ &=\mathbb{E}_{P_{X Y}}[log \frac{P(X,Y)}{P(X)P(Y)}] \\ &=\mathcal D_{K L}(P_{X Y}||P(X)P(Y)) \end{aligned} \tag 3 $$

因为互信息没办法精确的计算，但是已经有一些算法可以对其进行估计，作者首先使用了Mutual Information Neural Estimation（MINE）$^{[1]}$方法，其基于KL散度的 Donsker-Varadhan representation 给出了互信息的下限，如下公式：

$$ \mathcal{I}(X ; Y):=\mathcal{D}_{K L}(\mathbb{J}|| \mathbb{M}) \geq \widehat{\mathcal{I}}_{\omega}^{(D V)}(X ; Y):=\mathbb{E}_{\mathbb{J}}\left[T_{\omega}(x, y)\right]-\log \mathbb{E}_{\mathbb{M}}\left[e^{T_{\omega}(x, y)}\right] \tag 4 $$ 上式中的 $\mathbb{J}$ 表示 $X$ 和 $Y$ 的联合分布 $P_{X Y}$，$\mathbb{M}$ 表示 $X$ 和 $Y$ 的边缘分布的乘积 $P_{X}P_{y}$，$T_{\omega}$ 表示参数为 $\omega$ 的鉴别器。 更具体来说，这里的 $X$ 为图像的 feature map（ $f_{\psi}(X)$ ），$Y$ 为图像编码后的得到的 representation（$E_{\psi}(X)$）。 $P_{XY}$ 表示图片的 $f_{\psi}(X)$ 和其 $E_{\psi}(X)$ 之间的联合分布（因为来自同一张图片），而 $P_{ \tilde X}P_Y$ 表示另一张图片 $f_{\psi}(\tilde X)$ 和同一个 $E_{\psi}(X)$ 之间这两个边缘分布的乘积（因为来自不同的图片）。**前者需要最大化，而后者需要最小化**。因为鉴别器 $T_{\psi}$ 接收两个参数 $f_{\psi}(X) / f_{\psi}(\tilde X)$ 和 E_{\psi}(X)$，然后输出一个分数，表示有多大的把握确信这个 feature map 是对应于这个 representation的（即来自同一张图片），显然来自同一张图片的输出越大越好，来自不同图片的输出越小越好。

因此最大化 $\mathcal I(X;Y)$ 的目标变成了最大化其的下限 $\widehat{\mathcal{I}}_{\omega}^{(D V)}(X ; Y)$，而又转化为了一个对抗训练问题。这样，我们就可以写出这一目标的损失函数了，如下（$\psi$ 为编码器 $E$ 的参数，$\omega$ 为鉴别器的参数）：

$$ \begin{aligned} loss_G&=\underset{\omega, \psi}{\max} \widehat{\mathcal{I}}_{\omega}^{(D V)}(f_{\psi}(X);E_{\psi}(X)) \\ &=\underset{\omega, \psi}{\max} \mathbb{E}_{P_{XY}}\left[T_{\omega}(f_{\psi}(X),E_{\psi}(X))\right]-\log \mathbb{E}_{P_X×P_{\tilde X}}\left[e^{T_{\omega}(f_{\psi}(X),E_{\psi}(X))}\right] \\ &=\underset{\omega, \psi}{\min} -(\mathbb{E}_{P_{XY}}\left[T_{\omega}(f_{\psi}(X),E_{\psi}(X))\right]-\log \mathbb{E}_{P_X×P_{\tilde X}}\left[e^{T_{\omega}(f_{\psi}(X),E_{\psi}(X))}\right]) \end{aligned} \tag 5 $$

但由于我们的优化目标并不需要知道 MI 的具体估计值，而只需要能够将其最大化即可，所以我们不一定需要使用 KL 散度（也就是基于 DV representation 的方法），因此将上述损失函数可以写成更广泛的形式，如下：

$$ \begin{aligned} loss_G&=\underset{\omega, \psi}{\max}\widehat{\mathcal{I}}_{\omega}\left(f_{\psi}(X) ; E_{\psi}({X})\right) \\ &=\underset{\omega, \psi}{\min}-\widehat{\mathcal{I}}_{\omega}\left(f_{\psi}(X) ; E_{\psi}({X})\right) \end{aligned} \tag 6 $$

式子中的 $\widehat{\mathcal{I}}_{\omega}$ 可以换成其他的 MI 估计器，只要能给出 MI 的边界将其进行最大化即可。在文章中，作者尝试了 Jensen-Shannon MI estimator $^{[4]}$ 和 infoNCE $^{[5]}$ 两种方法，如下，并对其各自的优势与性能进行了比较分析：

$$ \widehat{\mathcal{I}}_{\omega, \psi}^{(\mathrm{JSD})}\left(X ; E_{\psi}(X)\right):=\mathbb{E}_{\mathbb{P}}\left[-\operatorname{sp}\left(-T_{\psi, \omega}\left(x, E_{\psi}(x)\right)\right)\right]-\mathbb{E}_{\mathbb{P} \times \tilde{\mathbb{P}}}\left[\operatorname{sp}\left(T_{\psi, \omega}\left(x^{\prime}, E_{\psi}(x)\right)\right)\right] \\ ,where \space sp(z)=log(1+e^z) \tag 7 $$ $$ \widehat{\mathcal{I}}_{\omega, \psi}^{(\mathrm{infoNCE})}\left(X ; E_{\psi}(X)\right):=\mathbb{E}_{\mathbb{P}}\left[T_{\psi, \omega}\left(x, E_{\psi}(x)\right)-\mathbb{E}_{\tilde{\mathbb{P}}}\left[\log \sum_{x^{\prime}} e^{T_{\psi, \omega}\left(x^{\prime}, E_{\psi}(x)\right)}\right]\right] \tag 8 $$

可以看到，我们上面得到的损失函数有一个下标 $G$，实际上就是代表这是 Global 情况下的目标。所谓 Gloabl ，也就是说我们是直接最大化整个图像的输入和输出之间的互信息的，在说什么是 Local Infomax 之前，再总结一下 Global Infomax 的流程：

（1）从数据集中取样原始图像 $x_+^{(1)},\dots,x_+^{(n)} \sim P_X$ ，然后计算 feature map $f_{\psi}(x_+^{(i)}) \forall_i $

（2）计算图像的 representation $y^{(i)}=h_{\psi}(f_{\psi}(x_+^{(i)}))$

（3）将 ${(f_{\psi}(x_+^{(i)}),y^{i})}$ 组成正样本对

（4）从数据集中取样不同的图像 $x_{-}^{(1)},\dots,x_{-}^{(n)} \sim P_X$，然后计算 feature map $f_{\psi}(x_{-}^{(i)}) \forall_i $

（5）将 ${(f_{\psi}(x_-^{(i)}),y^{i})}$ 组成负样本对

（6）通过优化编码器的参数 $\psi$ 和鉴别器的参数 $\omega$ 来最小化$-(\frac{1}{n} \sum_{i=1}^{n}T_{\psi}(f_{\psi}(x_+^{(i)}),y^{(i)}))-log \frac{1}{n} \sum_{i=1}^{n} e^{T_{\psi}(f_{\psi}(x_-^{(i)}),y^{(i)}))})$

Local Infomax

先说一下为什么要提出 Local Infomax？直觉上来看，对于一张图片来说，如果我们的下游任务不是重建类的任务，只是对图片进行分类，那么就没有必要对一些琐碎或者对分类任务无关紧要的像素。而如果我们的目标是最大化整张输入图片的 feature map 与 representation，那么编码器为了符合最后的全局最优情况，就有可能会选择到这些对下游任务并无实际作用的部分进行编码，这样得到的 representation 就肯定不会是针对下游任务最优的 representation。

而 Local Infoamx 的思想就是，我们并不将整张图片的 feature map 一次性输入损失函数来进行 MI 最大化，而是将其分为 $M×M$块（$M$ 不是指像素，而是指被分成了 $M^2$ 个块），一次输入一个块和同一个 representation，最终目标是使这 $M^2$ 个块和整张图片的 representation 的平均 MI 达到最大。这样就可以使给每个块之间共享的一些信息进行编码。

文章中也用实验证明了，根据下游任务的不同，Local Inofmax 在图像分类等一些下游任务中确实具有更好的效果。

因此，也就很容易写出 Local Infomax 的损失函数（与 $loss_G$ 的 $\omega$ 不是同一个）：

$$ \begin{aligned} loss_L&=\underset{\omega, \psi}{\max} \frac{1}{M^{2}} \sum_{i=1}^{M^{2}} \widehat{\mathcal{I}}_{\omega, \psi}\left(f_{\psi}^{(i)}(X) ; E_{\psi}(X)\right) \\ &=\underset{\omega, \psi}{\min} \frac{1}{M^{2}} -\sum_{i=1}^{M^{2}} \widehat{\mathcal{I}}_{\omega, \psi}\left(f_{\psi}^{(i)}(X) ; E_{\psi}(X)\right) \end{aligned} \tag 9 $$

总结一下 Local Infomax 的流程：

（1）从数据集中取样原始图像 $x_+^{(1)},\dots,x_+^{(n)} \sim P_X$ ，然后计算 feature map $f_{\psi}(x_+^{(i)}) \space \forall_i $ （2）计算图像的 representation $y^{(i)}=h_{\psi}(f_{\psi}(x_+^{(i)})) \space \forall_i$ （3）将 ${(f_{\psi}(x_+^{(i)})_j,y^{i})} \space \forall_j$ 组成正样本对 （4）从数据集中取样不同的图像 $x_{-}^{(1)},\dots,x_{-}^{(n)} \sim P_X$，然后计算 feature map $f_{\psi}(x_{-}^{(i)}) \forall_i $ （5）将 ${(f_{\psi}(x_-^{(i)})_j,y^{i})} \space \forall_j$ 组成负样本对 （6）通过优化编码器的参数 $\psi$ 和鉴别器的参数 $\omega$ 来最小化 $-\frac{1}{M^2} \sum_{j=1}^{M^2}(\frac{1}{n} \sum_{i=1}^{n}T_{\psi}(f_{\psi}(x_+^{(i)})_j,y^{(i)}))-log \frac{1}{n} \sum_{i=1}^{n} e^{T_{\psi}(f_{\psi}(x_-^{(i)})_j,y^{(i)}))})$

看起来和 Global Infomax 的流程差不多，主要是在第（3）（5）步中，现在需要对每个 patch 执行此操作（也就是Global的 $M^2$ 倍） ，而之所以只用 $j$ 来对 patch 进行索引，是因为 patch 在哪一行哪一列并不重要。第（5）步中的每个patch $j$ 则是来自另一张不同的图像。

Local Infomax的原理图如下：

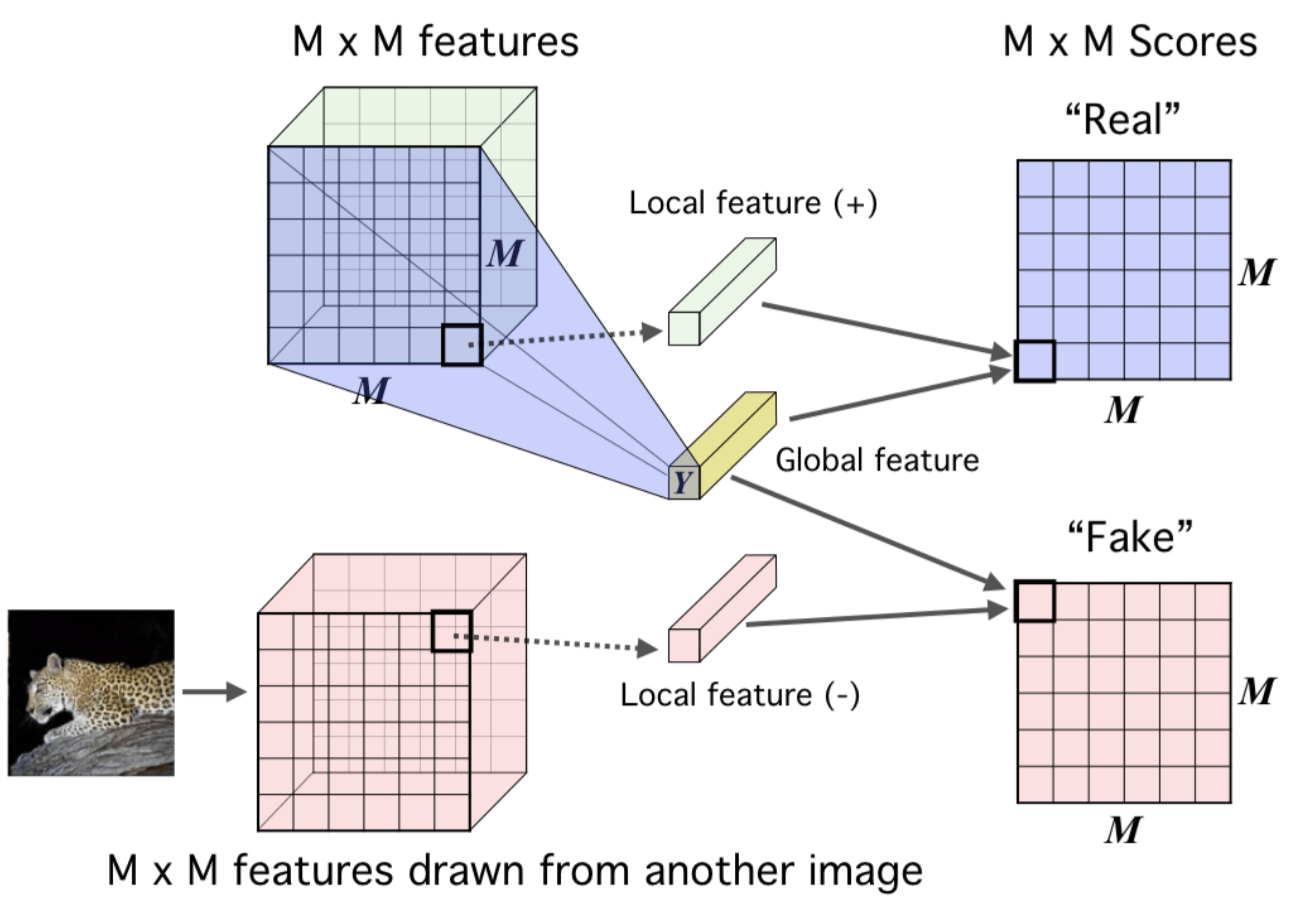
至于怎么计算这个平均互信息，文章的附录中给了两种方法，一个是直接将最后的 representation（$Y$）复制然后接到 feature map(+) 的块后面形成real，接到 feature map(-) 后面形成 fake，然后再利用一个 $1×1$ 的卷积鉴别器对对进行评分，如下图：

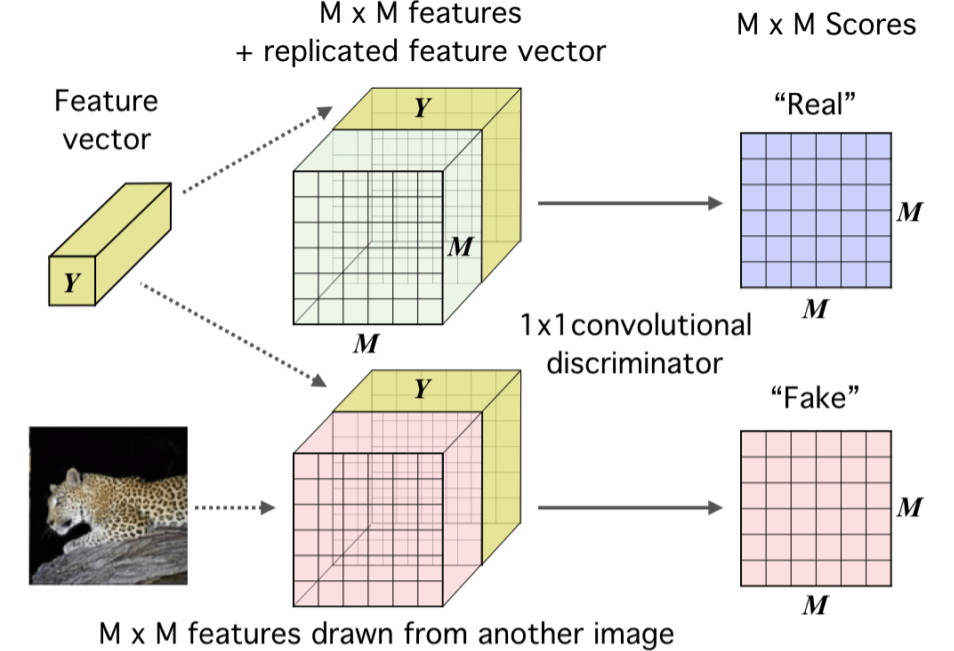
另一种方法则是利用点击运算，即对 representation（$Y$）进行全连接网络的编码，每个块用一个 $1×1$ 的网络进行编码，最后得到的两个结果是想同纬度的，然后进行点乘操作得到对应块的分数：

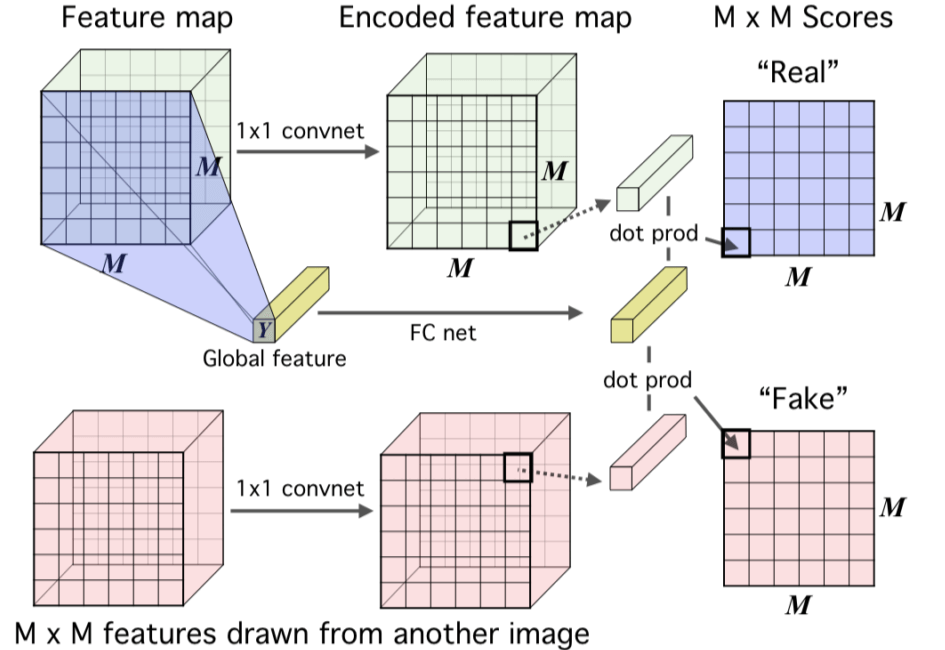
Matching representations to prior

若学习到的隐变量服从标准正态分布的先验分布，这有利于使得编码空间更加规整，甚至有利于解耦特征，便于后续学习。因此，在 DIM 中，我们同样希望加上这个约束，作者利用对抗自编码器（AAE）的思路引入对抗来加入这个约束，即训练一个新的鉴别器，而将编码器当做生成器。鉴别器的目标是区分 representation 分布的真伪（即是否符合先验分布），而编码器则是尽量欺骗判别器，输出更符合先验分布的 representation，如下图：

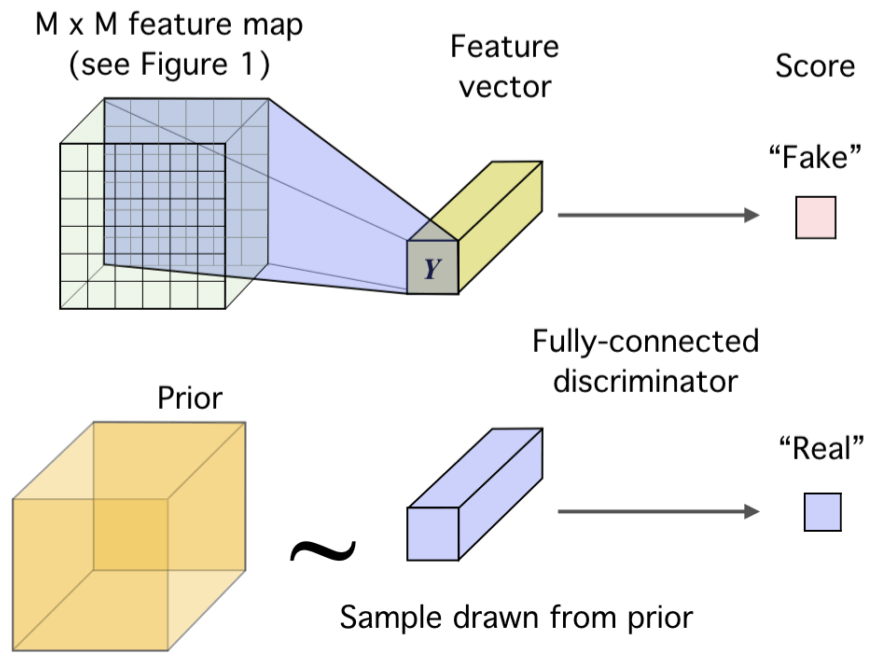
具体做法是，训练另一个鉴别器$D_{\phi}$，我们需要学习到一种 representation 来让这个鉴别器 $D_{\phi}$ 确信其来自先验分布 $Q_{prior}$，这不就是一种对抗的思想。

训练该鉴别器的损失函数如下：

$$ \begin{aligned} loss_{matching}&=\underset{\psi}{ \min } \underset{\phi}{ \max } \widehat{\mathcal{D}}_{\phi}\left(Q_{prior} \| Q_{\psi,X}\right) \\ &=\underset{\psi}{ \min } \underset{\phi}{ \max } \mathbb{E}_{Q_{prior}}\left[\log D_{\phi}(y)\right]+\mathbb{E}_{Q_{\psi,X}}\left[\log \left(1-D_{\phi}\left(E_{\psi}(x)\right)\right)\right] \end{aligned} \tag {10} $$

Final loss

将上面三个目标整合后，也就得到了 DIM 的最终目标，如下：

$$ \begin{aligned} &\underset{\omega_1, \psi}{\max} \alpha \widehat{\mathcal{I}}_{\omega_1}(f_{\psi}(X);E_{\psi}(X)) \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space (globa \space InfoMax)\\ &+\underset{\omega_2, \psi}{\max} \frac{\beta}{M^{2}} \sum_{i=1}^{M^{2}} \widehat{\mathcal{I}}_{\omega_2, \psi}\left(f_{\psi}^{(i)}(X) ; E_{\psi}(X)\right) \space\space\space (local \space InfoMax)\\ &+\underset{\psi}{ \min } \underset{\phi}{ \max } {\gamma}\widehat{\mathcal{D}}_{\phi}\left(Q_{prior} \| Q_{\psi,X}\right) \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space (prior \space matching) \\ &=\underset{\omega_1,\omega_2,\psi}{\min} (-\alpha\widehat{\mathcal{I}}_{\omega_1}(f_{\psi}(X);E_{\psi}(X)) - \frac{\beta}{M^{2}}\sum_{i=1}^{M^{2}} \widehat{\mathcal{I}}_{\omega_2, \psi}\left(f_{\psi}^{(i)}(X) ; E_{\psi}(X)\right)) + \underset{\psi}{ \min } \underset{\phi}{ \max } {\gamma}\widehat{\mathcal{D}}_{\phi}\left(Q_{prior} \| Q_{\psi,X}\right) \end{aligned} $$

之所以加上$\alpha、\beta、\gamma$三个参数，是因为有时候我们只想使用 global InfoMax (如重建类下游任务)，就可以将 $\beta$ 设置为0；而有时候只想使用 Iocal InfoMax (如分类任务)，就可以将 $\alpha$ 设置为0；但这两种情况下，最佳的$\gamma$是不同的，所以也需要 $\gamma$ 来进行调节。

References

[1] Ishmael Belghazi, Aristide Baratin, Sai Rajeswar, Sherjil Ozair, Y oshua Bengio, Aaron Courville, and R Devon Hjelm. Mine: mutual information neural estimation. arXiv preprint arXiv:1801.04062, ICML’2018, 2018.

[2] Alireza Makhzani, Jonathon Shlens, Navdeep Jaitly, Ian Goodfellow, and Brendan Frey. Adversarial autoencoders. arXiv preprint arXiv:1511.05644, 2015.

[3] Anthony J Bell and Terrence J Sejnowski. An information-maximization approach to blind separation and blind deconvolution. Neural computation, 7(6):1129–1159, 1995.

[4] Philemon Brakel and Y oshua Bengio. Learning independent features with adversarial nets for non-linear ica. arXiv preprint arXiv:1710.05050, 2017.

[5] Sebastian Nowozin, Botond Cseke, and Ryota Tomioka. f-gan: Training generative neural samplers using variational divergence minimization. In Advances in Neural Information Processing Systems, pp. 271–279, 2016.

[6] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018.