主要参考自 DR_CAN 的B站教程 纯干货傅里叶变换。
0x01 三角函数系的正交性与傅里叶级数
我们首先看一下这个定理: 组成三角级数的函数系
$$ \begin{aligned} 0(\text{sin}0x),1(\text{cos}0x),\text{sin}x,\text{cos}x,\text{sin}2x,\text{cos}2x,\dots,\text{sin}nx,\text{cos}nx \end{aligned} $$在 $[-\pi,\pi]$ 上正交,即其中任意两个不同的函数之积在 $[-\pi,\pi]$ 上的积分等于0,证明见附录1。
我们可以先记住这个结论,就是从上面的那组三角函数中随便选两个不同的三角函数,将他们的乘起来,然后在 $[-\pi,\pi]$ 下做积分,结果一定是0。
并且在三角函数系中两个相同的函数的乘积在 $[-\pi,\pi]$ 上的积分不等于0,且有:
$$ \begin{aligned} \int_{-\pi}^{\pi} \text{cos}nx·\text{cos}mx\text{dx} &= \int_{-\pi}^{\pi} \text{cos}^2nx\text{dx} \\ &=\int_{-\pi}^{\pi} \frac{1}{2}\left(1 +\text{cos}2nx\right)\text{dx} \\ &=\frac{1}{2} \left[\int_{-\pi}^{\pi}1\text{dx} + \int_{-\pi}^{\pi}\text{cos}2nx\text{dx}\right] \\ &=\pi \\ \end{aligned} $$ $$ \begin{aligned} \int_{-\pi}^{\pi} \text{sin}^2nx\text{dx} =\pi \\ \int_{-\pi}^{\pi} 1·1\text{dx}=2\pi \end{aligned} $$我们知道简单的周期运动可写作:$y=A\text{sin}(\omega t+\varphi)$ ,其中$A$ 为振幅,$\omega$ 为角频率,$\varphi$ 为初相。下图为 $\sin\left(x+\pi\right)$:
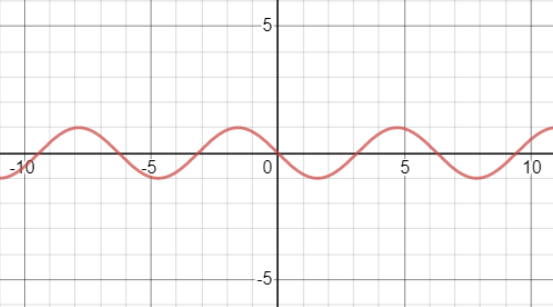
复杂的周期运动 $f(t)$ 可以看作简单周期运动的叠加。
下图为:$\sin\left(x+\pi\right)+\frac{1}{3}\sin\left(3x+\pi\right)+\frac{1}{5}\sin\left(5x+\pi\right)+\frac{1}{7}\sin\left(7x+\pi\right)+\frac{1}{9}\sin\left(9x+\pi\right)$
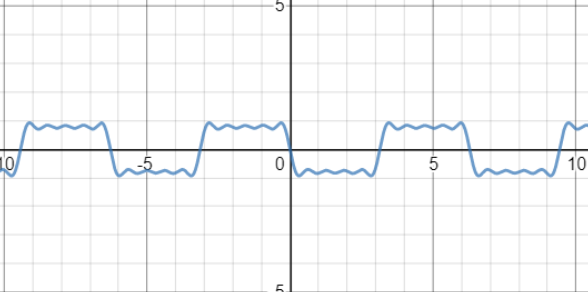
当累加的足够多,也就形成了一个周期性的方波。
因此周期函数 $f(t)$ 的表达式可写作:
$$ \begin{aligned} f(t)&=\sum_{n=0}^{\infty}A_n\text{sin}{(n\omega t+\varphi_n)} \\ &=A_0\text{sin}{\varphi_0}+\sum_{n=1}^{\infty}A_n\text{sin}{(n\omega t+\varphi_n)} \\ &=A_0\text{sin}{\varphi_0}+\sum_{n=1}^{\infty}\left[A_n\text{sin}{n\omega t}\text{cos}{\varphi_n} + A_n\text{cos}{n\omega t}\text{sin}{\varphi_n}\right] \end{aligned} $$我们令 $a_n=A_n\text{sin}{\varphi_n}$ , $b_n=A_n\text{cos}{\varphi_n}$, $\omega t=x$(这里我们假设周期为 $2\pi$,即$\omega=1$),代换后的周期函数表达式如下:
$$ \begin{aligned} f(x)&=A_0\text{sin}{\varphi_0}+\sum_{n=1}^{\infty}A_n\text{sin}{(n\omega t+\varphi_n)} \\ &=a_0+\sum_{n=1}^{\infty}(a_n\text{cos}{nx}+b_n\text{sin}{nx}) \\ \end{aligned} \tag{1} $$实际上,(1)式只是一个猜想式,我们需要找到 $a_0$、$a_n$ 和 $b_n$ 式该表达式成立。
首先求 $a_n$的表达式,可将(1)式两边同时乘以 $cosmx$,然后两边同时在 $[-\pi,\pi]$ 做积分,得到:
$$ \begin{aligned} \int_{-\pi}^{\pi}f(x)\text{cos}mx\text{dx}&=\int_{-\pi}^{\pi}a_0\text{cos}mx\text{dx}+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}a_n\text{cos}{nx}\text{cos}mx\text{dx}+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}b_n\text{sin}{nx}\text{cos}mx\text{dx} \\ &=a_0\int_{-\pi}^{\pi}\text{cos}mx\text{dx}+a_n\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}\text{cos}{nx}\text{cos}mx\text{dx}+b_n\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}\text{sin}{nx}\text{cos}mx \text{dx} \end{aligned} \tag{2} $$由前面证明的三角函数正交性可得:
$$ \begin{aligned} &\int_{-\pi}^{\pi}\text{cos}mx\text{dx}=\int_{-\pi}^{\pi}\text{cos}mx\text{sin}0x\text{dx}=0 \\ &\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}\text{sin}{nx}\text{cos}mx \text{dx}=0 \\ &\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}\text{cos}{nx}\text{cos}mx\text{dx}=0(n\neq m) \\ &\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}\text{cos}{nx}\text{cos}mx\text{dx}=\pi(n=m) \end{aligned} $$因此 (2) 式可以写作如下形式$(n=m)$:
$$ \begin{aligned} \int_{-\pi}^{\pi}f(x)\text{cos}mx\text{dx}&=\int_{-\pi}^{\pi}f(x)\text{cos}nx\text{dx} \\ &=a_n\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}\text{cos}{nx}\text{cos}mx\text{dx}\\ &=a_n\pi \\ \end{aligned} \tag{3} $$可以求得:
$$ \begin{aligned} a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\text{cos}nx\text{dx} \end{aligned} \tag{4} $$同理,我们将(1)式两边同时乘以 $sinmx$,然后两边同时在 $[-\pi,\pi]$ 做积分,可以求得:
$$ \begin{aligned} b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\text{sin}nx\text{dx} \end{aligned} \tag{5} $$同理,对(1)式两边同时在 $[-\pi,\pi]$ 做积分,可以求得:
$$ \begin{aligned} a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\text{dx} \end{aligned} \tag{6} $$对比(4)式和(6)式,不难看出当(4)式的 $n=0$ 时,它和 $a_0$ 只差了一个 $\frac{1}{2}$,因此为了将它们统一在一个表达式中,通常将(1)式写作如下的形式:
$$ \begin{aligned} f(x)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\text{cos}{nx}+b_n\text{sin}{nx}) \\ \end{aligned} \tag{7} $$最终得到的 (7) 式,就是三角级数的表示形式。当 $a_n$ 和 $b_n$ 由上面的 (4)(5) 式确定时,(7) 式即为 $f(x)$ 的傅里叶级数,称此时的 $a_n$ 和 $b_n$ 为傅里叶系数。(这里 $f(x)$ 周期为$2\pi$)
0x02 傅里叶级数的三角形式
上面我们推导傅里叶级数时,假设了周期为 $2\pi$ ,得到了如下形式的傅里叶级数:
$$ \begin{aligned} f(x)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\text{cos}{nx}+b_n\text{sin}{nx}) \\ &\left\{\begin{array}{ll} a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\text{cos}nx\text{dx} \\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\text{sin}nx\text{dx} \end{array}\right. \end{aligned} \tag {8} $$现在可以进一步推广至周期为 $T$,即 $f(t)=f(t+T)$,我们进行换元 $x=\frac{2\pi}{T}t$,$t=\frac{T}{2\pi}x$,然后令 $f(t)=f(\frac{2L}{\pi}x):= g(x)$,则有 $g(x)=g(x+2\pi)$。
所以可以将 $g(x)$ 用 (8) 式傅里叶级数展开:
$$ \begin{aligned} g(x)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\text{cos}{nx}+b_n\text{sin}{nx}) \\ &\left\{\begin{array}{ll} a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}g(x)\text{cos}nx\text{dx} \\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}g(x)\text{sin}nx\text{dx} \end{array}\right. \end{aligned} \tag {9} $$然后对 (9) 式再进行一次换元 $x=\frac{2\pi}{T}t$,得到:
$$ \begin{aligned} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\text{cos}{n\frac{2\pi}{L}t}+b_n\text{sin}{n\frac{2\pi}{L}t}) \\ &=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\text{cos}{n \omega t}+b_n\text{sin}{n \omega t}) \end{aligned} \tag{10} $$同理对 $a_n$ 和 $b_n$ 进行换元得到:
$$ \begin{aligned} a_n&=\frac{1}{\pi}\int_{-\pi}^{\pi}g(x)\text{cos}nx\text{dx} \\ &= \frac{1}{\pi}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\text{cos}{n\frac{2\pi}{T}t}\text{d}\frac{2\pi}{T}t \\ &=\frac{1}{\pi}\frac{2\pi}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\text{cos}{n\frac{2\pi}{T}t}\text{dt} \\ &=\frac{2}{T}\int_{0}^{T}f(t)\text{cos}{n \omega t}\text{dt} \end{aligned} \tag {11} $$ $$ \begin{aligned} b_n&=\frac{2}{T}\int_{0}^{T}f(t)\text{sin}{n \omega t}\text{dt} \end{aligned} \tag {12} $$综上,也就说明了任何周期函数都能用傅里叶级数来表示为三角函数的形式。对于周期函数 $f(t)$,周期为 $T$ ,角频率为$\omega_0=2\pi f_0=\frac{2\pi}{T}$,其三角形式的傅里叶级数如下:
$$ \begin{aligned} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\text{cos}{n \omega_0 t}+b_n\text{sin}{n \omega_0 t}) \\ &\left\{\begin{array}{ll} a_n=\frac{2}{T}\int_{0}^{T}f(t)\text{cos}{n \omega_0 t}\text{dt} \\ b_n=\frac{2}{T}\int_{0}^{T}f(t)\text{sin}{n \omega_0 t}\text{dt} \end{array}\right. \end{aligned} \tag {13} $$0x03 傅里叶级数的复指数形式
上一节我们推导了三角形式的傅里叶级数,其物理含义明确;但是实际操作上,指数形式的傅里叶级会更加便于数学处理,而且很容易与后面介绍的傅里叶变换统一起来。因此这一节我们就用欧拉公式将 (13) 式的傅里叶级数表示为复指数的形式。(欧拉公式的证明可见附录2)
首先,由欧拉公式 $e^{i\theta}=\text{cos}{\theta}+i\text{sin}{\theta}$ ,分别将 $\theta$ 和 $-\theta$ 代入其中再消元,得到三角函数的复指数形式如下:
$$ \begin{aligned} \text{cos}{\theta} = \frac{1}{2}\left(e^{i\theta}+e^{-i\theta}\right) \\ \text{sin}{\theta} = -\frac{1}{2}i\left(e^{i\theta}-e^{-i\theta}\right) \end{aligned} \tag {14} $$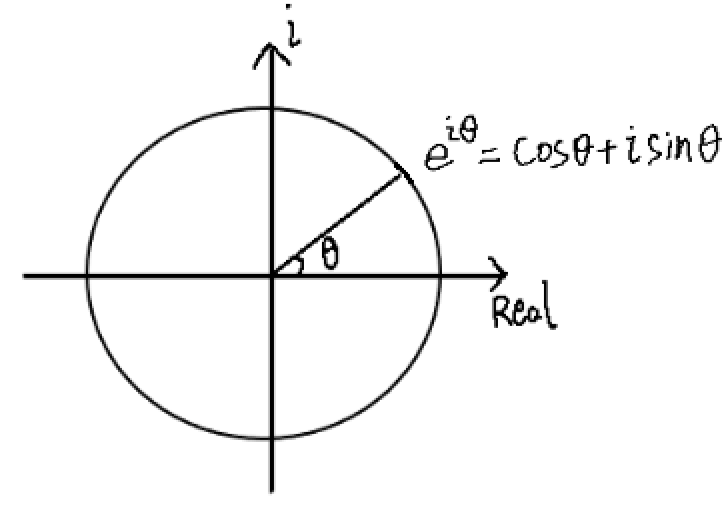
将 (14) 式的代入 (13) 式的傅里叶级数中得到:
$$ \begin{aligned} f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left[a_n\frac{1}{2}\left(e^{in \omega t}+e^{-in \omega t}\right)-b_n\frac{1}{2}i\left(e^{in \omega t}-e^{-in \omega t}\right)\right] \\ &=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left(\frac{a_n-ib_n}{2}e^{in \omega t}+\frac{a_n+ib_n}{2}e^{-in \omega t}\right) \\ &=\frac{a_0}{2} +\sum_{n=1}^{\infty}\frac{a_n-ib_n}{2}e^{in \omega t} +\sum_{n=1}^{\infty}\frac{a_n+ib_n}{2}e^{-in \omega t} \\ &=\sum_{n=0}^{0}\frac{a_0}{2}e^{0·i \omega t}+\sum_{n=1}^{\infty}\frac{a_n-ib_n}{2}e^{in \omega t} +\sum_{n=-1}^{-\infty}\frac{a_{-n} +ib_{-n}}{2}e^{in \omega t} \\ &=\sum_{n=-\infty}^{\infty} C_n e^{in \omega t} \\ where \space C_n=&\left\{\begin{array}{ll} \frac{a_0}{2},n=0 \\ \frac{a_n-ib_n}{2},n=1,2,3,\dots \\ \frac{a_{-n}+ib_{-n}}{2},n=-1,-2,-3,\dots \end{array}\right. \end{aligned} \tag {15} $$上面第 4 个等号第三项将 $n$ 换元为 $-n$,并将第一项写成单个累和的形式($e^{0·i \omega t}=1$);最后一个等号,可以看到三项的累和已经从$-\infty$ 加到了 $+\infty$,我们将 $e^{in \omega t}$ 提出来, 剩余项项用 $C_n$ 表示。
进一步计算 $C_n$ 的形式,将 (13) 式的傅里叶系数代入 $C_n$ 中得到:
(1)当 $n=0$ 时:
$$ \begin{aligned} C_n=\frac{a_0}{2}&=\frac{1}{2}\frac{2}{T}\int_{0}^{T}f(t)\text{dt} \\ &=\frac{1}{T}\int_{0}^{T}f(t)\text{dt} \\ &=\frac{1}{T}\int_{0}^{T}f(t)e^{-in \omega t}\text{dt} \end{aligned} \tag{16} $$上面的最后一个等号,因为在此情况下 $n=0$,所以加上 $e^{-in \omega t}$ 不改变结果。
(2)当 $n=1,2,3,\dots$ 时:
$$ \begin{aligned} C_n&=\frac{a_n-ib_n}{2}\\ &=\frac{1}{2}\left(\frac{2}{T}\int_{0}^{T}f(t)\text{cos}{n \omega t}\text{dt}-i\frac{2}{T}\int_{0}^{T}f(t)\text{sin}{n \omega t}\text{dt}\right) \\ &=\frac{1}{T}\int_{0}^{T}f(t) \left(\text{cos}{n \omega t}-i\text{sin}{n \omega t}\right)\text{dt} \\ &=\frac{1}{T}\int_{0}^{T}f(t)e^{-in \omega t}\text{dt} \\ \end{aligned} \tag{17} $$上面第3个等式可由欧拉公式得到: $\text{cos}{n \omega t}-i\text{sin}{n \omega t}=\text{cos}{(-n \omega t)}+i\text{sin}{(-n \omega t)}=e^{-in \omega t}$
(3)当 $n=-1,-2,-3,\dots$ 时:
$$ \begin{aligned} C_n&=\frac{a_{-n}+ib_{-n}}{2}\\ &=\frac{1}{2}\left(\frac{2}{T}\int_{0}^{T}f(t)\text{cos}{(-n \omega t)}\text{dt}+i\frac{2}{T}\int_{0}^{T}f(t)\text{sin}{(-n \omega t)}\text{dt}\right) \\ &=\frac{1}{2}\left(\frac{2}{T}\int_{0}^{T}f(t)\text{cos}{n \omega t}\text{dt}-i\frac{2}{T}\int_{0}^{T}f(t)\text{sin}{n \omega t}\text{dt}\right) \\ &=\frac{1}{T}\int_{0}^{T}f(t) \left(\text{cos}{n \omega t}-i\text{sin}{n \omega t}\right)\text{dt} \\ &=\frac{1}{T}\int_{0}^{T}f(t)e^{-in \omega t}\text{dt} \\ \end{aligned} \tag{18} $$观察 (16)(17)(18) 式,可以看到三个情况的最终结果竟然统一了!也就是对于 $ \forall n=0,±1,±2,±3,\dots$,有:
$$ \begin{aligned} C_n=\frac{1}{T}\int_{0}^{T}f(t)e^{-in \omega t}\text{dt} \end{aligned} \tag{19} $$综上,对于周期函数 $f(t)$,周期为 $T$,角频率为$w_0=2\pi f_0=\frac{2\pi}{T}$,其复指数形式的傅里叶级数为:
$$ \begin{aligned} &f(t)=\sum_{n=-\infty}^{\infty} C_n e^{in \omega_0 t}, \\ &C_n=\frac{1}{T}\int_{0}^{T}f(t)e^{-in \omega_0 t}\text{dt},n=0,±1,±2,±3,\dots \end{aligned} \tag {20} $$0x04 傅里叶变换
傅里叶变换实际上就是对傅里叶级数的进一步扩展,即不再要求 $f(t)$ 为周期函数,换句话也就是设周期 $T$ 趋于 $\infty$。
现在假设有一个周期为 $T$ 的函数 $f_T(t)=f_T(t+T)$,我们用复指数形式的傅里叶级数将其展开得到:
$$ \begin{aligned} &f_T(t)=\sum_{n=-\infty}^{\infty} C_n e^{in \omega_0 t}, \\ &C_n=\frac{1}{T}\int_{0}^{T}f_T(t)e^{-in \omega_0 t}\text{dt},n=0,±1,±2,±3,\dots \end{aligned} \tag {21} $$其中 $\omega_0=\frac{2 \pi}{T}$ 称为基频率。可以看到,实际上是由 $C_n$ 区分不同函数的,因为对于任意的傅里叶变换都是 $C_n$ 乘对应的复指数,再累和。假设 $f_T(t)$ 的时域图像如下:
我们画出它在复平面上的频域图像如下:
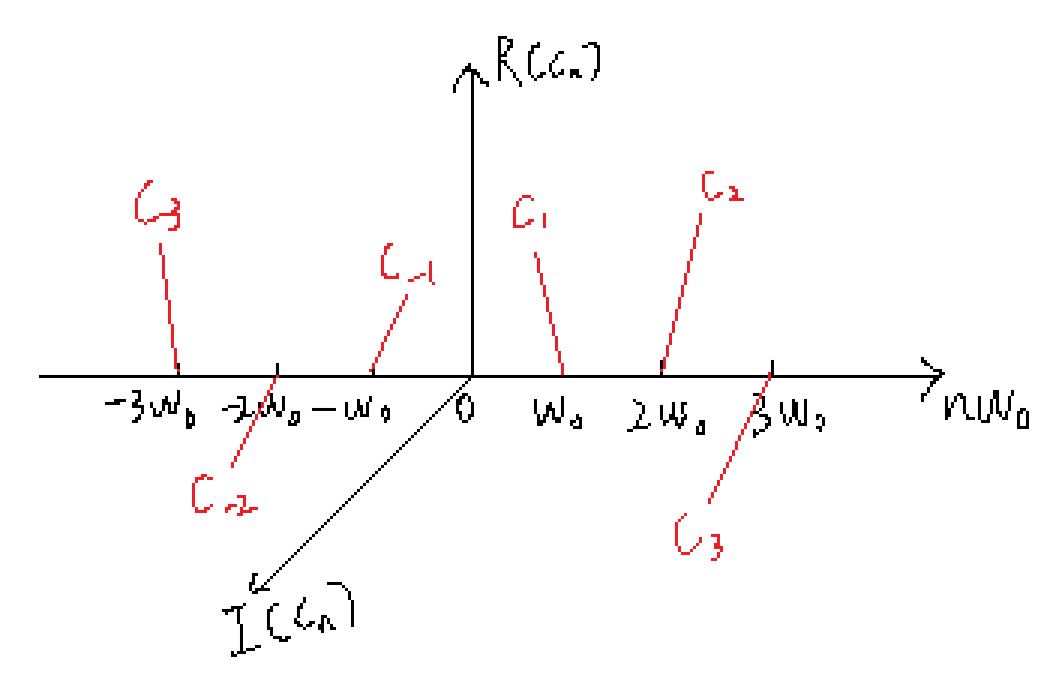
如果觉得上面这张三维复平面下的频域图不好理解,可以参考下面这张图(来自@李泽光一个相关回答里的图,图中 $X_n$ 与这里的 $C_n$ 含义类似):
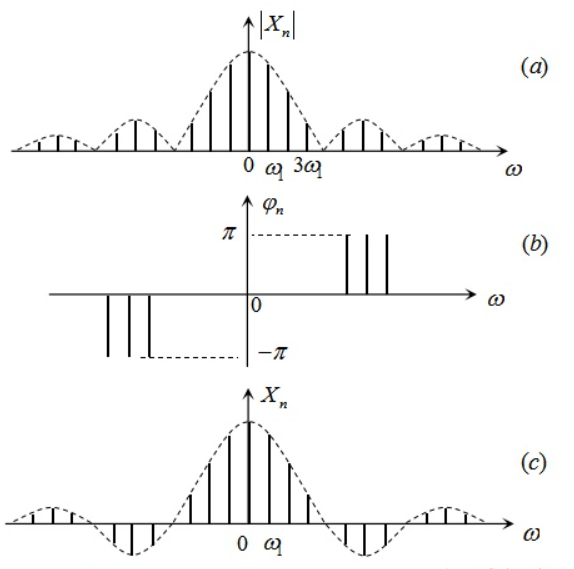
所谓傅里叶级数就是将时域下的周期连续函数(上图),转换为频域上的非周期离散函数(下图),也就是说对于频域图像做运算: $\dots,C_{-2}e^{-2i \omega_0t}+C_{-1}e^{-i \omega_0t}+C_{0}e^{0}+C_{1}e^{ i\omega_0t}+C_{2}e^{2i \omega_0t},\dots$ 也就能得到时域下的函数图像。
而傅里叶变换要做的就是将时域下的非周期连续函数转换到频域上的非周期连续函数。
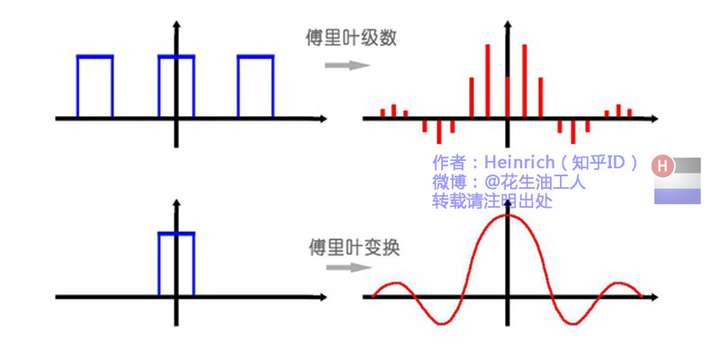
前面说了非周期函数可以将其看作周期无限大($T→\infty$),也就是 $\lim_{T→\infty}f_T(t)=f(t)$
我们令频域图像上的间隔为 $\Delta \omega=(n+1)\omega_0-n\omega_0=\omega_0=\frac{2\pi}{T}$,当 $T→+\infty$ 时,$\Delta→-\infty$。从图像上看也就意味着每个 $C_i$ 之间的距离越来越来小,极限情况频域图像每个 $C_i$ 就挨在一起了,也就变成了连续的形式;并且离散情况下的横轴 $n\omega_0$,在连续的情况下就可以用一个连续的变量 $\omega$ 表示。
进一步推导,将 (19) 式中的 $C_n$ 代入 $f_T(t)$ ,且 $T=\frac{2\pi}{\Delta \omega}$:
$$
\begin{aligned}
f(t)&=\sum_{n=-\infty}^{\infty} \frac{1}{T}\int_{0}^{T}f(t)e^{-in \omega_0 t}\text{dt} e^{in \omega_0 t} \
&=\sum_{n=-\infty}^{\infty} \frac{\Delta \omega}{2\pi}\int_{0}^{T}f_T(t)e^{-in \omega_0 t}\text{dt} e^{in \omega_0 t}
\end{aligned} \tag {22}
$$
对于 (22) 式,当我们令 $T→\infty$ 时,相应的有 $\int_{0}^{T}dt→\int_{-\infty}^{+\infty}$,$n\omega_0→\omega$,$\sum_{n=-\infty}^{\infty}\Delta\omega→\int_{-\infty}^{+\infty}d\omega$,得到:
$$
\begin{aligned}
f(t)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t)e^{-i \omega t}\text{dt} e^{i \omega t}\text{d}\omega
\end{aligned} \tag {23}
$$
最后,我们令上面 (23) 式的中间部分为为 $F(\omega)$ 如下:
$$
\begin{aligned}
F(w)&=\int_{-\infty}^{\infty}f(t)e^{-i \omega t}\text{dt}
\end{aligned} \tag {24}
$$
得到的 (24) 式即为傅里叶变换,而原来的 (23) 式即为傅里叶逆变换,可写成如下形式:
$$
\begin{aligned}
f(t)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega) e^{i \omega t}\text{d}\omega
\end{aligned} \tag {25}
$$
附录1:三角函数正交性证明
当 $n≠m$时,由积化和差及牛顿莱布尼茨公式得:
$$ \begin{aligned} \int_{-\pi}^{\pi} \text{cos}nx·\text{cos}mx\text{dx} &= \int_{-\pi}^{\pi} \frac{1}{2}\left[\text{cos}(nx-mx) + \text{cos}(nx+mx)\right]dx \\ &=\frac{1}{2} \left[\int_{-\pi}^{\pi}\text{cos}(n-m)x\text{dx} + \int_{-\pi}^{\pi}\text{cos}(n+m)x\text{dx}\right] \\ &=\frac{1}{2} \left[\frac{1}{n-m}\text{sin}(n-m)x\bigg|_{-\pi}^{\pi}+ \frac{1}{n+m}\text{sin}(n+m)x\bigg|_{-\pi}^{\pi} \right] \\ &=0 \end{aligned} $$ $$ \begin{aligned} \int_{-\pi}^{\pi} \text{cos}nx·\text{sin}mx\text{dx} &= \int_{-\pi}^{\pi} \frac{1}{2}\left[\text{sin}(nx+mx) - \text{sin}(nx-mx)\right]dx \\ &=\frac{1}{2} \left[\int_{-\pi}^{\pi}\text{sin}(n+m)x\text{dx} + \int_{-\pi}^{\pi}\text{sin}(n-m)x\text{dx}\right] \\ &=0 \end{aligned} $$同理:
$$ \begin{aligned} \int_{-\pi}^{\pi} \text{sin}nx·\text{cos}mx\text{dx} &= 0 \\ \int_{-\pi}^{\pi} \text{sin}nx·\text{sin}mx\text{dx} &= 0 \end{aligned} $$当 $n=m$ 时,
$$ \begin{aligned} \int_{-\pi}^{\pi} \text{cos}nx·\text{sin}mx\text{dx} &= \int_{-\pi}^{\pi} \text{sin}nx·\text{cos}mx\text{dx} \\ &=\int_{-\pi}^{\pi} \text{sin}nx·\text{cos}nx\text{dx} \\ &=\int_{-\pi}^{\pi} \frac{1}{2}\left[\text{sin}2nx+sin0x\right]\text{dx} \\ &=\frac{1}{2}\int_{-\pi}^{\pi}\text{sin}2nx\text{dx} \\ &=0 \end{aligned} $$附录2:欧拉公式的证明
欧拉公式:$e^{i\theta}=\text{cos}{\theta}+i\text{sin}{\theta}$
证明:
首先,令
$$ \begin{aligned} f(\theta)=\frac{e^{i\theta}}{\text{cos}{\theta}+i\text{sin}{\theta}} \end{aligned} $$对上式进行求导得到:
$$ \begin{aligned} f'(\theta)&=\frac{ie^{i\theta}(\text{cos}{\theta}+i\text{sin}{\theta})-e^{i\theta}(-\text{sin}{\theta}+i\text{cos}{\theta})}{(\text{cos}{\theta}+i\text{sin}{\theta})^2} \\ &=\frac{ie^{i\theta}\text{cos}{\theta}-e^{i\theta}\text{sin}{\theta}+e^{i\theta}\text{sin}{\theta}-ie^{i\theta}\text{cos}{\theta}}{(\text{cos}{\theta}+i\text{sin}{\theta})^2} \\ &=0 \end{aligned} $$因为 $f’(\theta)=0$,说明 $f(\theta)$ 为一个常数,不妨设 $\theta=0$,则:
$$ \begin{aligned} f(\theta)=f(0)=\frac{e^{i0}}{\text{cos}{0}+i\text{sin}{0}}=1 \end{aligned} $$所以得证:
$$ \begin{aligned} &f(\theta)=\frac{e^{i\theta}}{\text{cos}{\theta}+i\text{sin}{\theta}}=1 \\ &e^{i\theta}=\text{cos}{\theta}+i\text{sin}{\theta} \end{aligned} $$