1 算法分析
1.1 渐近分析的记号



1.2 主定理
主定理方法应用于如下的递归形式:$T(n) = aT(n/b) + f (n) $,其中,$a\geq1, b \geq 1$,$f$ 是渐近正的。


2 分治与递归
2.1 阶乘函数

代码:
1 | //阶乘函数 |
2.2 Fibonacci数列

代码:
1 | // Fibonacci数列 |
2.3 全排列问题

思路:
- 定义函数
perm(int list[], int k, int m)表示获取list[k:m]的全排列。 - 递归条件:
- 当
n=1时,全排列只有一种,即为它本身。 - 当
n>1时,可以依次将每一个数作为前缀,然后对后续n-1个数进行全排列。
- 当
代码:
1 | // 全排列 |
2.4 整数划分问题


(1)递归解法
思路:对整数n进行划分,将最大加数不大于m的划分个数记作 $q(n,m)$
对于$q(n,m)$:
当
n=1,m=1时,整数划分只有一种结果当
n<m时,q(n,m)等价于q(n,n)当
n=m时,共有1+q(n,m-1)中划分结果:- 整数划分中包含
m,则只有一种划分结果,即{m} - 整数划分中不包含
m,则意味着划分中的最大整数位m-1,即需递归解决q(n,m-1)
- 整数划分中包含
当
n>m时,共有q(n-m,m)+q(n,m-1)中划分结果- 整数划分中包含
m,即划分为{m,{..},这其中除了m外,其余部分可以看成对n-m继续进行划分,最大值可能为m,需递归解决q(n-m,m) - 整数划分中不包含
m,即划分结果中最大为m-1,递归解决q(n,m-1)
- 整数划分中包含
代码:
1 | //整数划分问题(递归解法) https://developer.aliyun.com/article/445250 |
(2)动态规划解法
TODO
2.5 棋盘覆盖问题

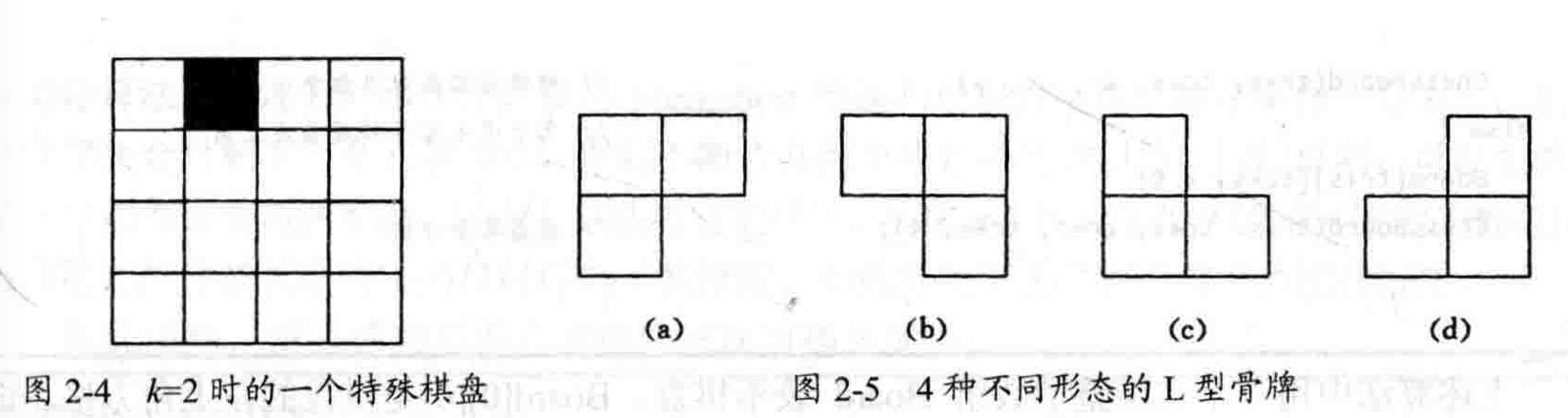
思路:
分治法将棋盘划分为四个区域,从而得到四个子问题进行解决。
特殊方格必然位于四个区域中的其中一个,但是另外三个区域则没有特殊方格,导致了子问题不相同。因此,可以假设先用一个L型骨牌放在四个区域的交界处当作特殊方格,从而使每一个区域内都存在一个特殊方格,如下图所示:
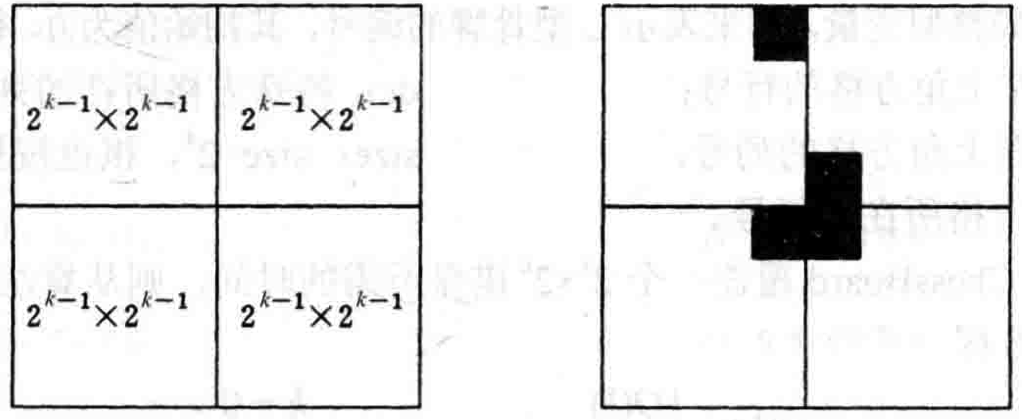
通过这样的分割和假设,棋盘分割问题就可以转化为四个1/4规模的子问题。
代码:
1 | //棋盘覆盖问题 |
2.6 归并排序
递归的解法:
- 先对
nums[l:m]进行排序,再对nums[m+1:r]进行排序。 - 将排好序的两部分合并,合并的时候先创建一个临时
tmp,然后依次比较两部分的数值大小,将较小的放入tmp,然后移动指针;如果某一部分的元素已经全部放入,将另一部分剩余元素直接放入即可。
1 | /* |
2.7 整数因子分解问题

1 | 1: 1 |
(1)解法一:递归
思路:
- 当
n=1时,只有一种分解方式。 - 当
n>1时,solve(n)可以对n的每一个因子再去求该分解子问题。
1 |
|
3 动态规划
3.1 矩阵连乘问题

(1)最优子结构
将$A_i A_{i+1} \dots A_j$的矩阵连乘定义为$A[i:j]$,那么现假设在位置$k$ 加括号使$A[i:j]=A[i:k]A[k+1:j]$,那么总计算量就等于$A[i:k]$的计算量加上$A[k+1:j]$的计算量,再加上这矩阵相乘的计算量$p_{i-1}p_k p_j$。
并且,计算$A[i:j]$的最优次序所包含的计算矩阵子链$A[1:k]$和$A[k+1:j]$的次序也是最优的,即具有最优子结构性质。
反证:如果$k$不是最优的,即存在一个更好的划分位置$k’$使$A[1:k’]$或$A[k’+1:j]$的计算量更少,那么得到的$A[1:n]$计算量也会比最优次序的计算量更少,导致矛盾。
(2)建立递归关系
用$m[i][j]$存储$A[i][j]$的最优次序计算量,则原问题的最优值为$m[1][m]$。
- 当$i=j$时,只有一个矩阵,因此$m[i][j]=0$
- 当$i<j$时,假设在$k$断开,则$m[i][j]=m[i][k]+m[k+1][j]+p_{i-1} p_k p_j$,由于$k$的位置不确定,因此这里需要取$min$。
递归式如下:
$$
m[i][j]= \begin{cases}0 & i=j \ \min {i \leqslant k<j}\left{m[i][k]+m[k+1][j]+p{i-1} p_{k} p_{j}\right} & i<j\end{cases}
$$
除此之外,还可以顶一个$s[i][j]$用来存储最优断开位置$k$,在计算出最优值$m[i][j]$后,可递归地由$s[i][j]$构造出相应的最优解。
(3)构造最优解
s[i][j]记录了A[i:j]最佳断开的位置k,因此当求解A[1:n]的最优加括号方式,只需要递归得查找A[i:k]和A[k+1][j]得最优加括号方式,即A[1:s[1][n]]和A[s[1][n]+1:n]。
(4)算法复杂度为$O(n^3)$

代码:
1 | // 矩阵连乘 |
3.2 最长公共子序列

(1)最优子结构
设序列$X_m={x_1,x_2,\dots,x_m}$和$Y_n={y_1,y_2,\dots,y_n}$的最长公共子序列为$Z_k={z_1,z_2,\dots,z_k}$,可以从后往前看:
- 如果$x_m=y_n$,那么这个数一定在公共子序列中,即$z_k=x_m=y_n$,那么原问题的规模下降为求解$X_{m-1}$和$Y_{n-1}$的最长公共子序列$Z_{k-1}$
- 如果$x_m \neq y_n$且$z_k \neq x_m$,那么$x_m$一定不在公共子序列中,因此原问题规模可以下降为求解$X_{m-1}$和$Y_n$的最长公共子序列$Z_k$
- 如果$x_m \neq y_n$且$z_k \neq y_n$,那么$y_n$一定不在公共子序列中,因此原问题规模可以下降为求解$Y_{n-1}$和$X_m$的最长公共子序列$Z_k$
反证:
- 如果$z_k \neq x_m$,那么也就说明$z_k$后面还有一个公共数,即${z_1,z_2,\dots,z_k,x_m}$,那么此时公共子序列的长度为$k+1$,与$Z_k$是$X$和$Y$的最长公共子序列矛盾,因此必有$z_k=x_m=y_n$。同样的,如果$X_{m-1}$和$Y_{n-1}$有长度大于$k-1$的公共子序列$W$,那么将$x_m=y_n$加在该序列末尾,会导致$X_m$和$Y_n$的最长公共子序列长度大于$k$,矛盾。因此,$Z_{k-1}$是$X_{m-1}$和$Y_{n-1}$的最长公共子序列。
- 因为$z_k \neq x_m$,$Z_k$是$X_{m-1}$和$Y$的公共子序列,若$X_{m-1}$和$Y$有长度大于$k$的公共子序列$W$,则$W$应该也是$X_m$和$Y_n$的公共子序列,与$Z_k$是$X_m$和$Y_n$最长公共子序列矛盾。
因此,最长公共子序列问题包含了两个序列前缀的最长公共子序列的子问题,且具有最优子结构的性质。
(2)构造递归方程
- 如果$x_m=y_n$,那么这个数一定在公共子序列中,此时只需要找到$X_{m-1}$和$Y_{m-1}$的最长公共子序列,再在其末尾加上$x_m(x_m=y_n)$即可。
- 如果$x_m \neq y_n$,那么就需要在$X_{m-1}$和$Y_n$以及$X_m$和$Y_{n-1}$两个最长公共子序列子问题中,找出更大的那个序列。
递归方程如下,$c[i][j]$表示$X_i$与$Y_j$的最长公共子序列长度:
$$
c[i][j]= \begin{cases}
0 & i>0 ; j=0 \
c[i-1][j-1]+1 & i, j>0 ; x_{i}=y_{i} \
\max {c[i][j-1], c[i-1][j]} & i, j>0 ; x_{i} \neq y_{i}\end{cases}
$$
(3)最优解
如果除了LCS的长度,还想获取具体的LCS序列,则还需要一个$b[i][j]$用来记录当前采取了哪种子问题,从而在构造LCS的时候,可以递归地进行打印。
代码:
1 | // 最长公共子序列 |
3.3 最大字段和

(1)分治法:
将原问题$a[1:n]$的最大子段和分解为$a[1:n/2]$和$a[n/2+1,n]$的两个子问题,分别求这两个子问题的最大子段和。
在这两个子问题进行合并的时候,会存在以下三种情况:
- $a[1:n]$的最大子段和与子问题$a[1:n/2]$的最大子段和相同。
- $a[1:n]$的最大子段和与子问题$a[n/2+1:n]$的最大子段和相同。
- $a[1:n]$的最大子段和$\sum_{k=i}^j{a_k}$的开始位置$i<n/2$,结束位置$j>n/2+1$。
对于前两种情况,直接递归求解即可。对于第三种情况,$a[n/2]$和$a[n/2+1]$肯定在最优子段中,那么只需从位置$n/2$分别向前、向后找到最大的子段,也就是
$$
最大子段和=\max_{1 \leq i \leq n/2} \sum_{k=i}^{n/2}a[k] + \max_{n/2+1 \leq i \leq n} \sum_{k=n/2+1}^{j}a[k]
$$复杂度分析:子问题规模为$n/2$,合并需要$O(n)$,递归式如下,解得$T(n)=O(n\log{n})$
$$
T(n) =
\begin{cases}
O(1) & n \leq c \
2T(n/2) + O(n) & n \gt c\end{cases}
$$
代码:
1 | // 最大子段和 |
(2)动态规划
设$b[i-1]$表示$a[1:i-1]$的最大子段和,那么对于第$i$个元素$a[i]$来说,它要么合并到$a[1:i-1]$的最大子段中,要么重新成为一个新的子段,取决于$b[i-1]+a[i]$和$a[i]$的大小。
因此,动态规划的递归式如下:
$$
b[i] = \max { b[i-1] + a[i], a[i]},\space 1 \leq i \leq n
$$
该方法只需要遍历一次序列,复杂度为$O(n)$
代码:
1 | // 最大子段和 |
动态规划的遍历方式通常是以序列的结束节点为基准,如下:

3.4 凸多边形最优三角剖分

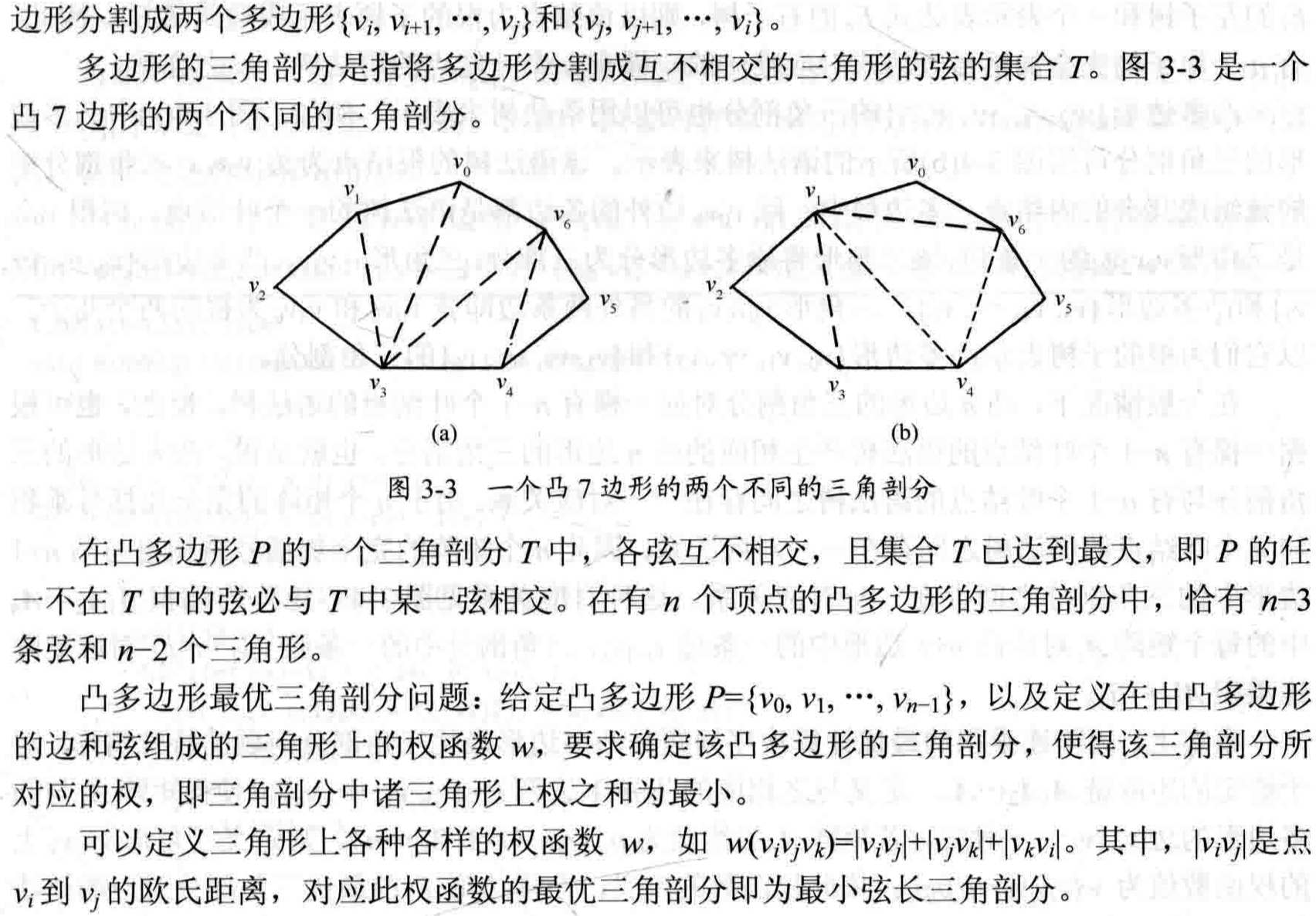
思路:
本质上与矩阵连乘问题类似,定义$t[i][j](1 \leq i \lt j \leq n)$ 为凸多边形 ${v_{i-1},v_i,\dots,v_j }$ 的最优三角剖分对应的权函数值。因此,原问题计算凸$n+1$边形的最优权值为$t[1][n] ({v_0,v_1,\dots,v_n})$。
若只有两条边,定义权值为零,即$t[i][i]=0(i=1,2,\dots,n)$。
当至少有三个顶点时($j-i\ge 1$)时,以$v_{i-1}v_j$的弦底边,某一个点$v_k$为顶点,将凸多边形划分成了${v_{i-1},v_{i}\dots,v_k}$和${v_{k},v_{k+1},\dots,v_j}$两个凸多边形,以及一个三角形${v_{i-1},v_k,v_j}$,这两个划分出来的凸多边形构成了子问题$t[i][k]$和$t[k+1][j]$,且具有最优子结构性质。
因此,原问题$t[i][j]$就等于了$t[i][k]+t[k+1][j]$再加上三角形的权值$w(v_{i-1} v_k v_j)$。而现在不确定最优划分的$v_k$的位置,所以$t[i][j]$的递归式定义如下,时间复杂度为$O(n^3)$:
$$
t[i][j]= \begin{cases}0 & i=j \ \min {i \leqslant k \leqslant j}\left{t[i][k]+t[k+1][j]+w\left(v{i-1} v_{k} v_{j}\right)\right} & i<j\end{cases}
$$若想构造最优三角剖分,还需要定一个数组$s[i][j]$用于记录$v_k$的顶点位置,时间复杂度为$O(n)$
代码:
1 | void MinWeightTriangulation(int n, vector<vector<int>> &t, vector<vector<int>> &s) |
3.5 多边形游戏

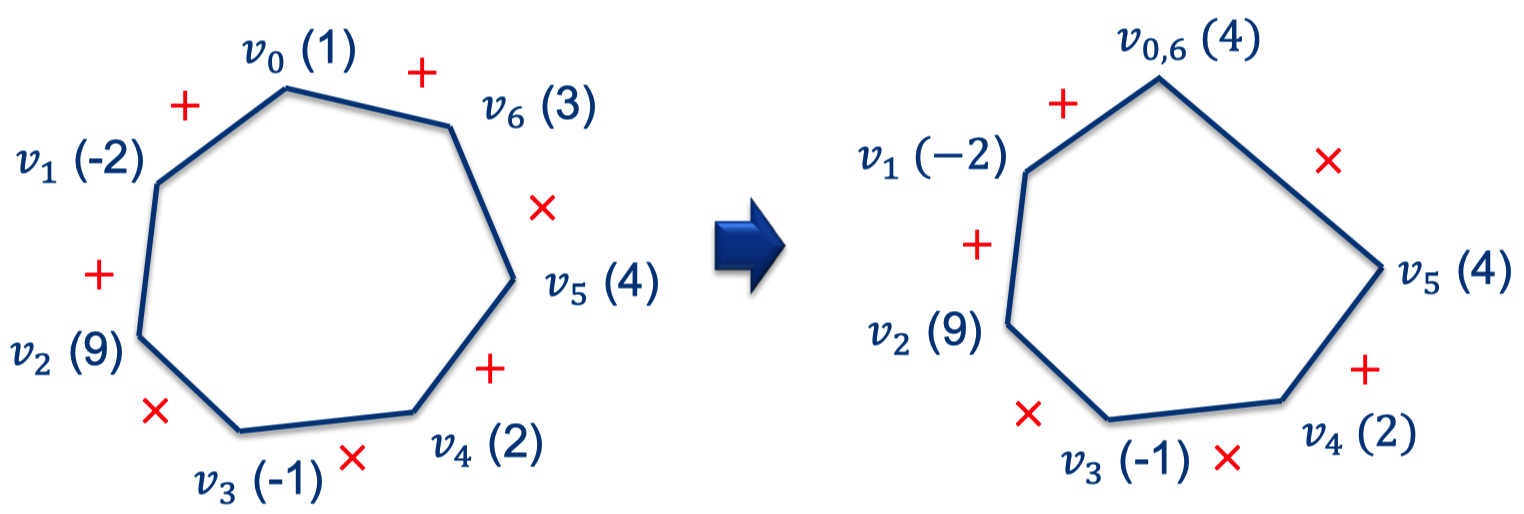
书上讲的挺清楚,直接放上来。



3.6 图像压缩
在计算机中,常用像素点的灰度值序列${p_1,p_2,\dots, p_n}$表示图像。其中整数$p_i(1 \leq i \leq n)$,表示像素点$i$的灰度值($0 \sim 255$),因此最多需要8位表示一个像素。
图像压缩就是将像素点序列${p_1,p_2,\dots, p_n}$分割成$m$个连续段$S_1,S_2,\dots,S_m$。
其中$S_i$中有$l[i]$个像素,且该段中每个像素都只用$b[i]$位表示,也就是“要表示该段中最大的数字需要的位数”,这样每一个像素段就可以用$l[i]*b[i]$位来存储。
除此之外,还需要用一定的存储空间来表示每一段的$b[i]$和$l[i]$的值,$b[i]$最大为8,也就是需要3位来表示,如果限制$l[i]$的最大值位256,那么就需要8位来表示。
因此,每一段子序列$S_i$所需要的存储空间就为$l[i]*b[i]+11$,总共需要的存储空间为$\sum_{i=1}^{m}l[i]b[i]+11m$
现在图像压缩问题,就是确定像素序列${p_1,p_2,\dots, p_n}$的最优分段,使得依此分段所需的存储空间最小。其中,$0 \leq p_i \leq 256, \space 1 \leq i \leq n$,每个分段长度不超过256位。
(1)最优子结构(?)
假设$l[i]$和$b[i]$($1 \leq i \leq m$)是${p_1,p_2,\dots,p_n}$的一个最优分段。显然$l[1]、b[1]$是${p_1,\dots,p_{l[1]}}$的一个最优分段,且$l[i]$和$b[i]$($2 \leq i \leq m$ )是${p_{l[1]+1},\dots,p_n }$的一个最优分段,即满足最优子结构性质。
(2)递归计算最优值
设$s[i]$($1 \leq i \leq n$)是像素序列${p_1,p_2,\dots,p_i}$的最优分段所需要的存储位数,以下面这个例子说明:

- $s[0]$:当没有像素的时候肯定为0,也就是$s[0]=0$
- $s[1]$:当像素序列长度为1时,直接用该段所需的最大存储位(上例位3),再加上用于存储b和l的11
- $s[2]$:当像素序列长度大于2时,就考虑在哪里进行分段,并取下面这些情况的最小值:
- 不分段,即将这2个像素看成一段,那么还是用该段所需的最大存储位数(3)乘上该段的像素数量(2),再加上11。
- 从$p_1$后面分段,前面一段的最优存储空间直接用$s[1]$表示;第二段用该段所需的最小存储位数(3)乘上该段的像素数量(1),再加上11。
- $s[3]$:当计算序列长度为3的最优存储空间,依然是寻找在哪里进行分段,此时有三种情况,取其中的最小值:
- 不分段,将前3个像素看成一段,就是直接用该段所需的最大存储位数(3)乘上该段的像素数量(3),再加上11。
- 从$p_1$后面分段,前面一段的最优存储空间直接用$s[1]$表示;第二段用该段所需的最大存储位数(3)乘上该段的像素数量(2),再加上11。
- 从$p_2$后面分段,前面一段的最优存储空间直接用$s[2]$表示;第二段用该段所需的最大存储位数(3)乘上该段的像素数量(1),再加上11。
- 以此类推,知道计算出$s[n]$即为$p_1,\dots,p_n$的最优分段所需的存储空间。
因此,递归式为:
$$
\begin{gathered}
s[i]=\min _{1 \leqslant k \leqslant \min {i, 256}}{s[i-k]+k * b \max (i-k+1, i)}+11 \
\operatorname{bmax}(i, j)=\left[\log \left(\max {i \leqslant k \leqslant j}\left{p{k}\right}+1\right)\right]
\end{gathered}
$$
上式中$bmax(i,j)$就是为了找到${p_i,\dots,p_j}$段中所需要的存储位数。
(3)代码:
1 | void Compress(int n, int p[], int s[], int l[], int b[]) |
3.7 流水作业调度

完成集合 $S$ 中作业所需的最短时间为 $T(S,t)$,表示机器 $M_1$ 开始加工 $S$ 中作业时,机器 $M_2$ 还需要等待 $t$ 时间后才可用,因此原问题的最优值为 $T(N,0)$。
(1)最优子结构
设原问题 $N = {1,2,\dots,n}$ 的最优调度为 $\pi$ (即$n$个作业的一个排列),所需加工时间为 $a_{\pi(1)}+T(S,b_{\pi(1)})$,其中子问题 $S=N-{\pi(1)}$。若 $S$ 存在更优的调度 $T’(S,b_{\pi(1)})$,即 $T’(S,b_{\pi(1)})< T(S,b_{\pi(1)})$,那么可以得到$a_{\pi(1)}+T’(S,b_{\pi(1)}) < a_{\pi(1)}+T(S,b_{\pi(1)})$,与 $\pi$ 是原问题的最优解矛盾,所以该问题满足最优子结构形式。
(2)构造递归方程
当$T(S,t)$加工第 $i$ 个作业时,$M_1$ 上需要需要时间 $a_i$, $M_2$ 开始加工第 $i$ 个作业前,需要等待 $\max {t,a_i}-a_i=\max {t-a_i, 0}$ 个时间,然后再需要$b_i$ 时间完成作业 $i$ 的加工,因此递归方程如下:
$$
T(S,t) = \min_{i \in S} {a_i+T(S-{i},b_i + \max{t-a_i,0})}
$$
(3)基于 Johnson 法则的流水调度算法
流水调度问题一定存在满足 Johnson 法则的最优调度,算法如下:
令 $N_1={i|a_i < b_i}$,$N_2 = {i| a_i \geq b_i}$
将 $N_1$ 中的作业依 $a_i$ 非减序排列,将 $N_2$ 中的作业依 $b_i$ 非增序排列。
- $M_2$ 上任务等待的时间越少越好 => 在 $M_1$ 上加工时间短的排前面,在 $M_2$加工时间长的排在前面。
$N_1$中作业接 $N_2$ 中作业构成满足 Johnson 法则的最优调度
算法复杂度为 $O(nlogn)$


3.8 0-1背包问题

(1)最优子结构
设 $(y_1,y_2,\dots,y_n)$ 是原问题 $\max \sum_{i=1}^{n}v_i x_i, \sum_{i=1}^{n}w_ix_i \leq c$的最优解,则 $(y_2,\dots,y_n)$其子问题为 $\max \sum_{i=2}^{n}v_i x_i, \sum_{i=2}^{n}w_ix_i \leq c-w_1y_1$。否则,若子问题存在一个更优的解 $(z_2,\dots,z_n)$,即 $\sum_{i=2}^{n}v_i z_i \gt \sum_{i=2}^{n}v_i y_i$,那么可以得到 $v_1 y_1 + \sum_{i=2}^{n}v_i z_i \gt v_1 y_1 + \sum_{i=2}^{n}v_i y_i$,与 $(y_1,y_2,\dots,y_n)$ 是原问题的最优解矛盾,所以该问题满足最优子结构性质。
(2)构造递归方程
该问题的最优值为 $m(i,j)$ 表示背包容量为 $j$,可选择物品为 $i,i+1,\dots,n$ 时的0-1背包问题最优值,其递归式如下:
$$
\begin{gathered}
m(i, j)= \begin{cases}\max \left{m(i+1, j), m\left(i+1, j-w_{i}\right)+v_{i}\right} & j \geqslant w_{i} \
m(i+1, j) & 0 \leqslant j<w_{i}\end{cases} \
m(n, j)= \begin{cases}v_{n} & j \geqslant w_{n} \
0 & 0 \leqslant j<w_{n}\end{cases}
\end{gathered}
$$
(3)计算复杂性分析
该递归式需要 $O(nc)$ 的计算时间(算法相当于填一个二维表,行列分别是物品数量和背包最大容量)
(4)算法的改进

改进后的算法复杂性为 $O(2^n)$
4 贪心算法
证明贪心选择策略
4.1 活动安排问题

(1)贪心选择策略
每次将结束时间最早的活动优先安排,即留下尽可能多的时间给其他活动。
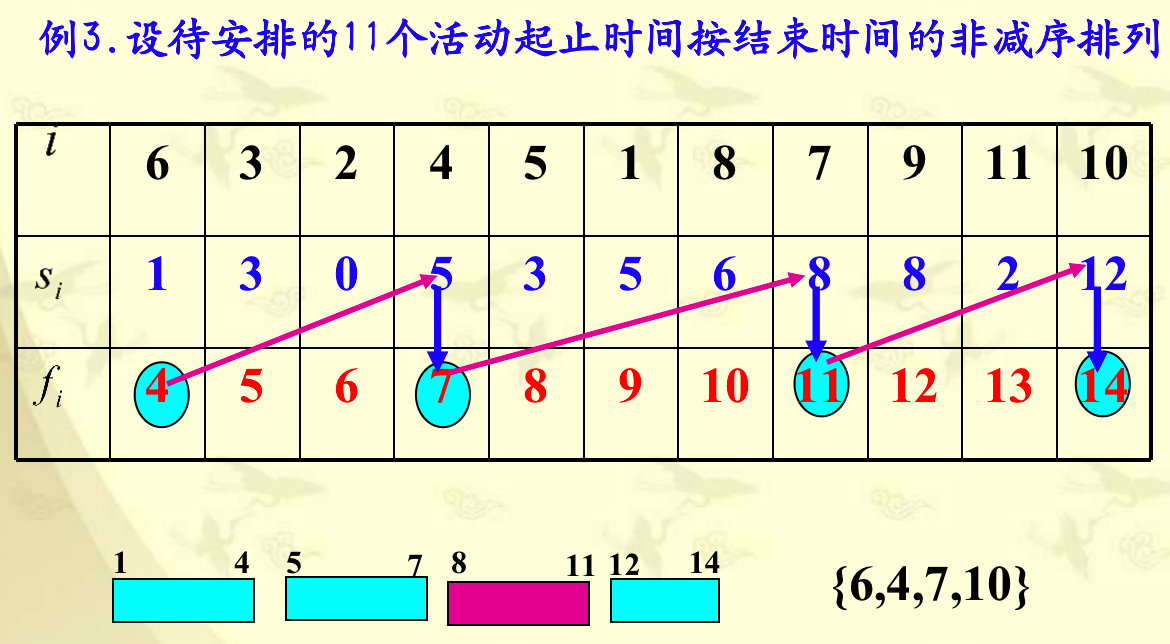
具体做法为,按活动的结束时间非减序排列,然后在安排完第一个活动后,以此判断后续活动是否与前一个安排的活动结束时间相容,相容则安排,不相容则不安排。
证明:设原问题 $E={1,2,\dots,n}$ 为所给活动集合,其中活动按结束时间非减序排列,即活动1具有最早完成时间。设该问题的的最优解为 $A$,且 $A$ 中的活动按结束时间 $f_i$ 非减序排列,$A$ 中第一个活动是活动 $k$。
- 若 $k=1$,则 $A$ 为一个以贪心选择开始的最优解。
- 若 $k \gt 1$,则设 $B=A - {k} \cup {1} $,(即用第1个活动替换第k个活动)因为 $f_1 \leq f_k$ 且 $A$ 中的活动是相容的,所以 $B$ 中的活动也是相容的。又因为 $|B|=|A|$,且 $A$ 是最优的,所以 $B$ 也是最优的,也就是说 $B$ 是以贪心选择活动 1 开始的最优活安排。
- 综上,从存在以该贪心选择开始的最优活动安排方案。
(2)最优子结构
设子问题 $E’= {i \in E: s_i \geq f_1}$,若 $A$ 是原问题 $E$ 的最优解, 则 $A’=A-{1}$ 是子问题 $E’$ 的最优解。若$E’$ 存在更优的一个解 $A’’$,即 $A’’ < A’$,那么有 $A’’ \cap {1}<A’ \cap {1}=A$,与 $A$ 是原问题的最优解矛盾,所以该问题满足最优子结构性质。
(3)复杂度分析
按结束时间排序活动需要$O(n logn)$,按贪心算法安排活动需要$O(n)$,总共需要 $O(n long)$
代码:
1 | //假设已经按结束时间非减序 |
4.2 背包问题

与0-1背包问题的区别是,背包问题可以选择物体的一部分装入背包,因此可以使用贪心算法。
贪心策略是每次优先将单位重量价值高的物品装入背包内。
0-1背包由于每个物品只能选择装入或者不装入,如果使用贪心策略可能会导致背包容量的浪费,从而总价值达不到最优。
代码:
1 | // 背包问题 |
4.3 最优装载

(1)贪心选择策略
重量最轻的优先进行装载。
证明:设集装箱按照其重量非减序排列, $(x_1,x_2,\dots,x_n)$ 是原问题的一个最优解,设 $k= \min_{1 \leq i \leq n} {i|x_i=1}$,(第一个装入的集装箱为k),如果原问题有解,则 $1\leq k \leq n$。
- 当 $k=1$ 时,$(x_1,x_2,\dots,x_n)$ 是满足贪心选择性质的一个最优解。
- 当 $k \gt 1$ 时,取另一个解$(y_1,y_2,\dots,y_n)$ ,其中 $y_1=1,y_k=0,y_i=x_i,1 \lt i \leq n,i \neq k$,(也就是用第1个箱子替换掉原来装入的第k个箱子),又因为 $w_1 \leq w_k$,所以有 $\sum_{i=1}^{n}w_iy_i=\sum_{i=1}^{n}w_ix_i-w_k+w_1 \leq \sum_{i=1}^{n}w_ix_i \leq c$,即 $(y_1,y_2,\dots,y_n)$ 是装载问题的可行解,且 $\sum_{i=1}^{n}y_i=\sum_{i=1}^{n}x_i$,即$(y_1,y_2,\dots,y_n)$ 是满足贪心选择性质的最优解。
- 所以,装载问题具有贪心选择性质。
(2)最优子结构性质
设 $A={x_1,x_2,\dots,x_n}$ 是原问题 $n$ 个集装箱 $E$ 的最优解,则 $A’=(x_2,x_3,\dots,x_n)$ 是子问题 $x_1=1$,轮船载重量$c-w_1$ 的子问题的最优解。若存在子问题更优的一个解 $A’’$,使得 $\sum_{x \in A’’} x_i \lt \sum_{x \in A’} x_i$,则可以得到 $x_1 + \sum_{x \in A’’} x_i \lt x_1 + \sum_{x \in A’} x_i = \sum_{x \in A} x_i$,与 $A$ 是原问题的最优解矛盾。因此,装载问题具有最优子结构性质。
(3)算法复杂度
重要复杂度来自于对集装箱重量的排序,即 $O(n \log{n})$。
代码:
1 | // 对物品按照重量非减序排序 |
4.4 哈夫曼编码
贪心选择性质:每次选择频率最小的两棵子树进行合并,从而产生一棵新的子树,其频率为合并的两棵子树频率之和。n 个字符的哈夫曼算法复杂度为 $O(n \log{n})$。
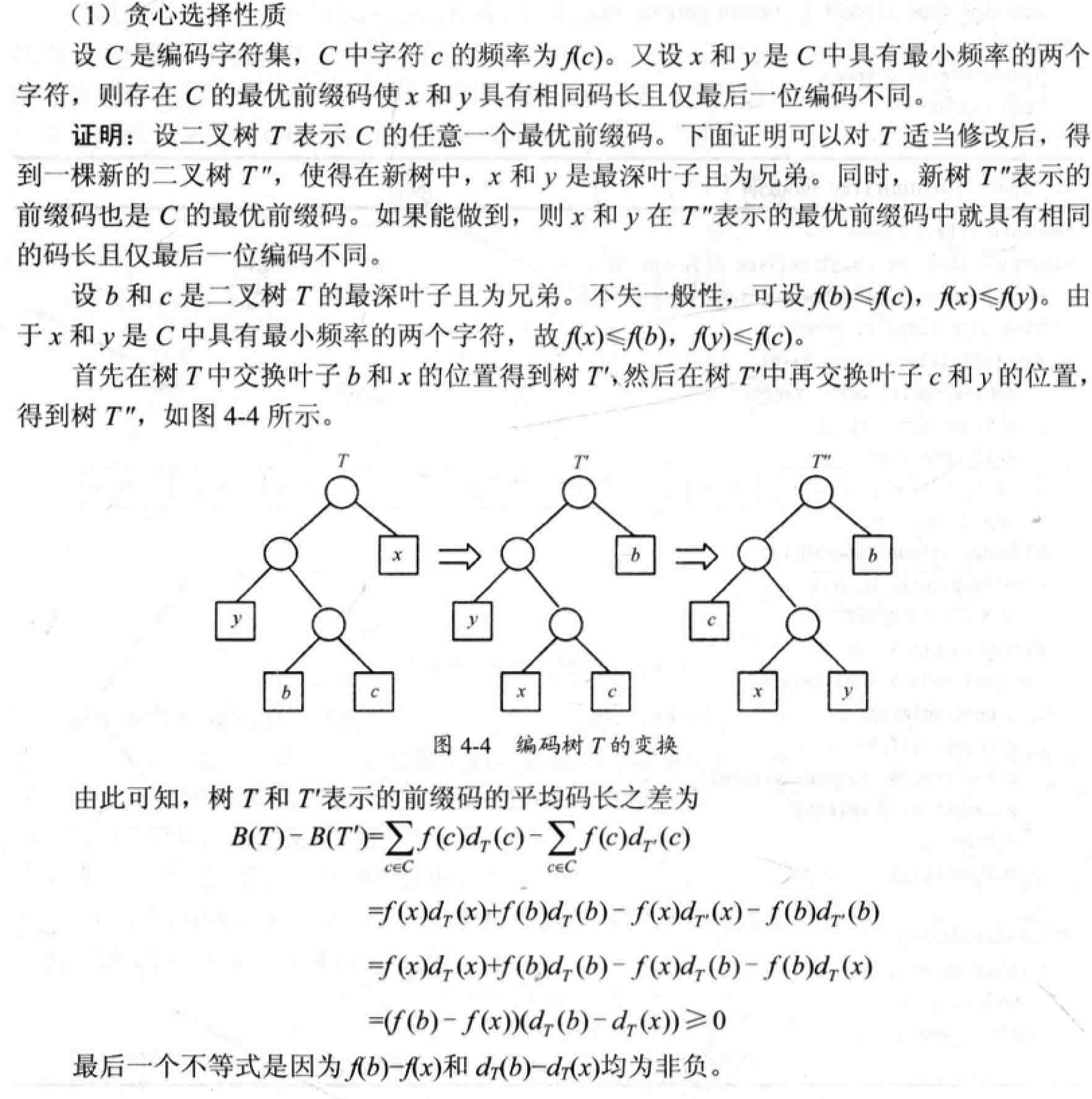

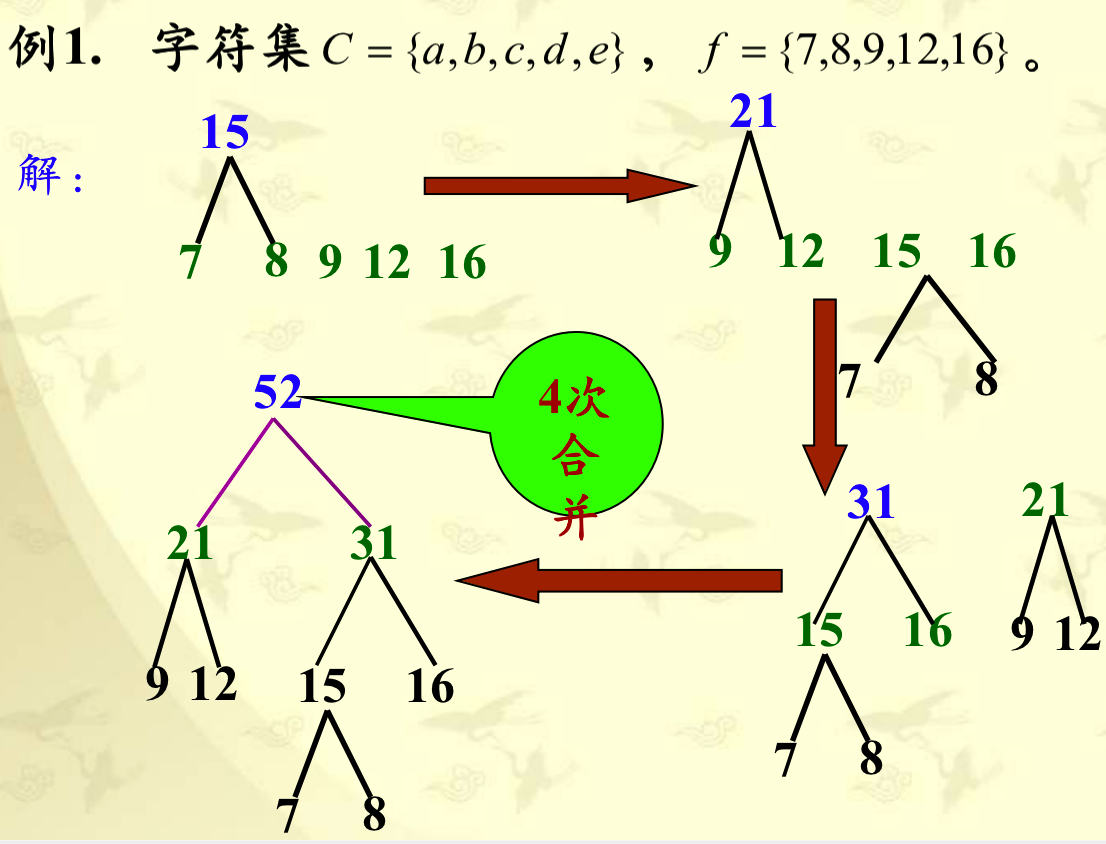
哈夫曼编码的实例,频率小的字符深度大:
4.5 单源最短路径

最优子结构性质:一个最短路径的子路径也是最短路径
算法基本思想——贪心:
- 维护一个顶点集合 $S$,它们从原点 $s$ 的最短路径已知
- 每一步添加 𝑣 ∈ 𝑉 − 𝑆 中具有最小距离的顶点到 S 中
- 更新剩余顶点 v 的距离估计
Dijkstra算法(边权重非负,如果权重可能为负则采用Bellman-Ford算法):
- 初始时,S中仅含有源
- 设 v 是 G 的某一个顶点,把从源到 v 且中间只经过 S 中顶点的路 称为从源到 v 的特殊路径,并用数组 dist 记录当前每个顶点所对 应的最短特殊路径长度
- 每次从 V-S 中取出具有最短特殊路长度的顶点 v,将 v 添加到 S 中 ,同时对数组 dist 作必要的修改
- 一旦 S 包含了所有 V 中顶点,dist 就记录了从源到所有其它顶点 之间的最短路径长度
- 对于具有 $n$ 个顶点和 $e$ 条边的带权有向图,主循环需要 $O(n)$,循环执行 n-1次,所以复杂度为 $O(n^2)$。
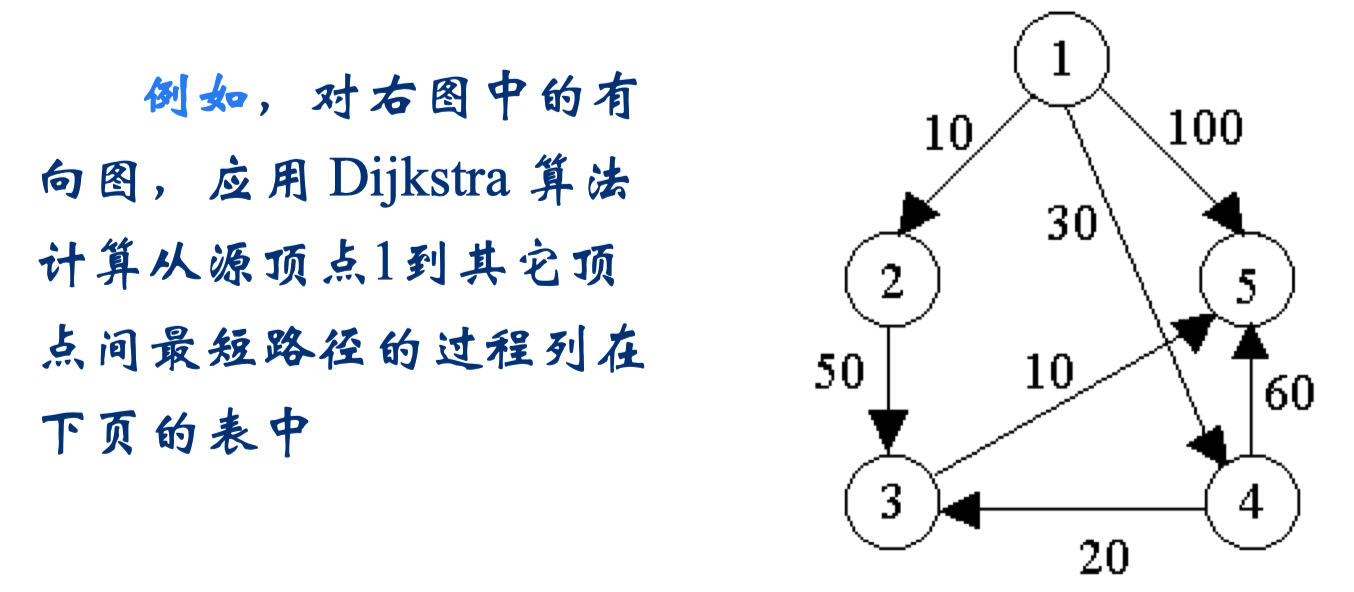
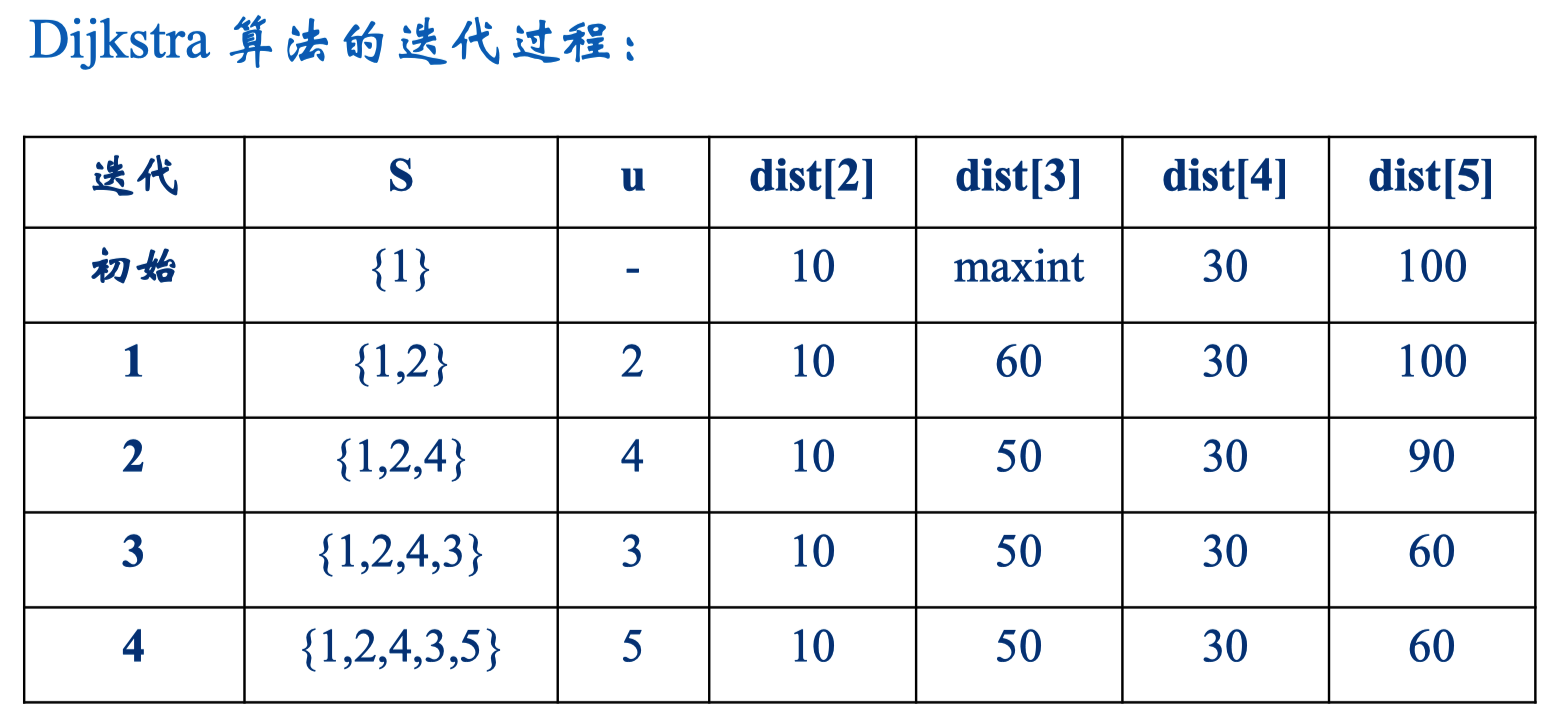
Dijkstra算法的贪心选择策略是从 V - S 中选择具有最短特殊路径的顶点 u,从而确定从源到 u 的最短路径长度 dist[u]。


4.6 最小生成树

(1)Prim 算法(选边)
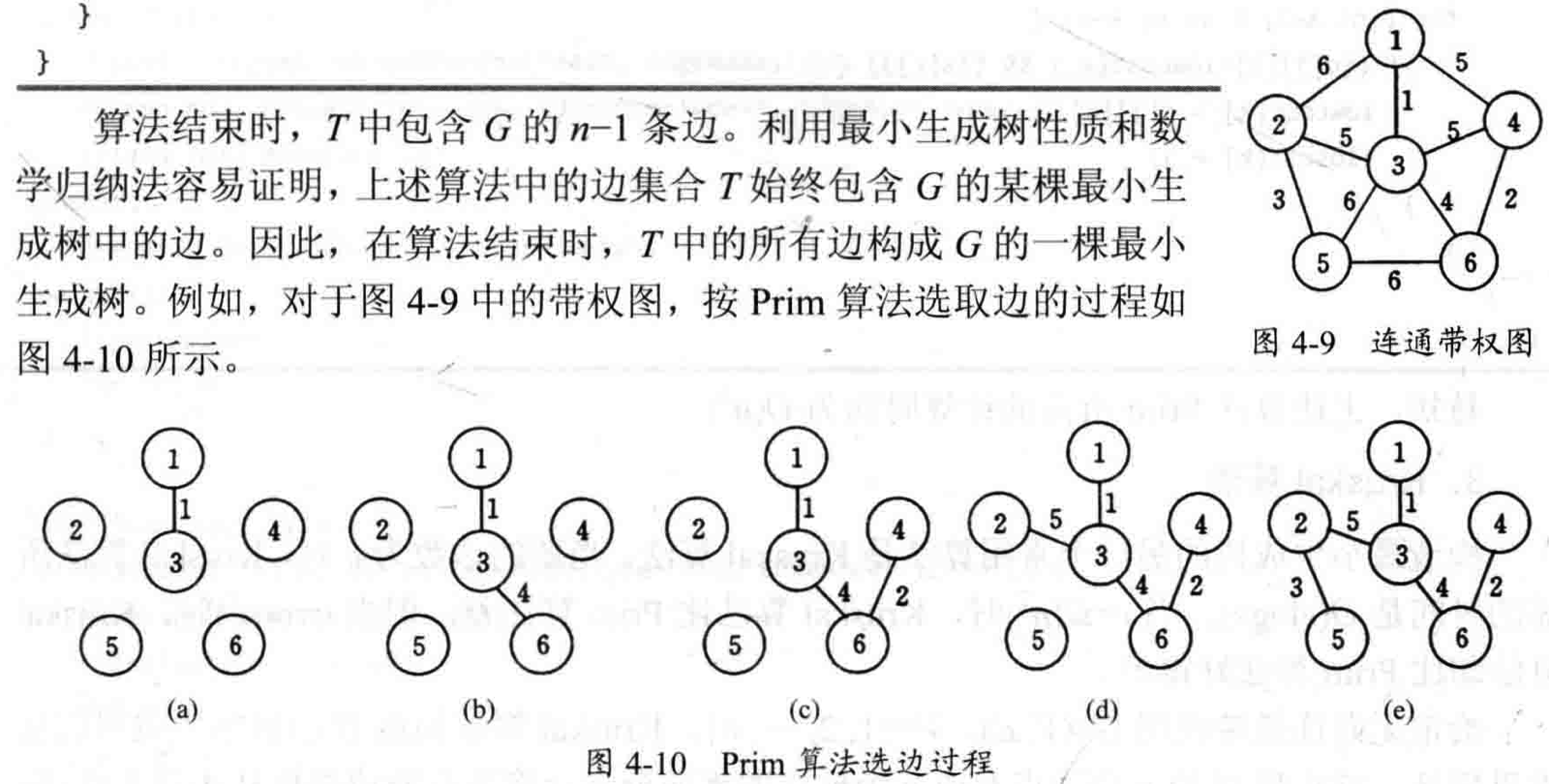
设 $G=(V,E)$ 是连通带权图,$V={1,2,\dots,n}$。构造 $G$ 的最小生成树的 Prim算法基本思想是: 首先设置 $S={1}$,然后只要 $S$ 是 $V$ 的真子集,就做如下贪心选择:选取满足条件 $i \in S$,$j \in V-S$,且 $c[i][j]$ 最小的边,并将顶点 $j$ 添加到 $S$ 中。这个过程一直进行直到 $S=V$ 时为止,选取到的所有边恰好构成 $G$ 的一颗最小生成树。
贪心选择性质证明:上述算法中的边集合 T 始终包含 G 的某棵最小生成树中的边 (循环不变式)。因此,在算法结束时,T 中的所有边构成 G 的 一棵最小生成树
Prim 算法的时间复杂度为 $O(n^2)$。
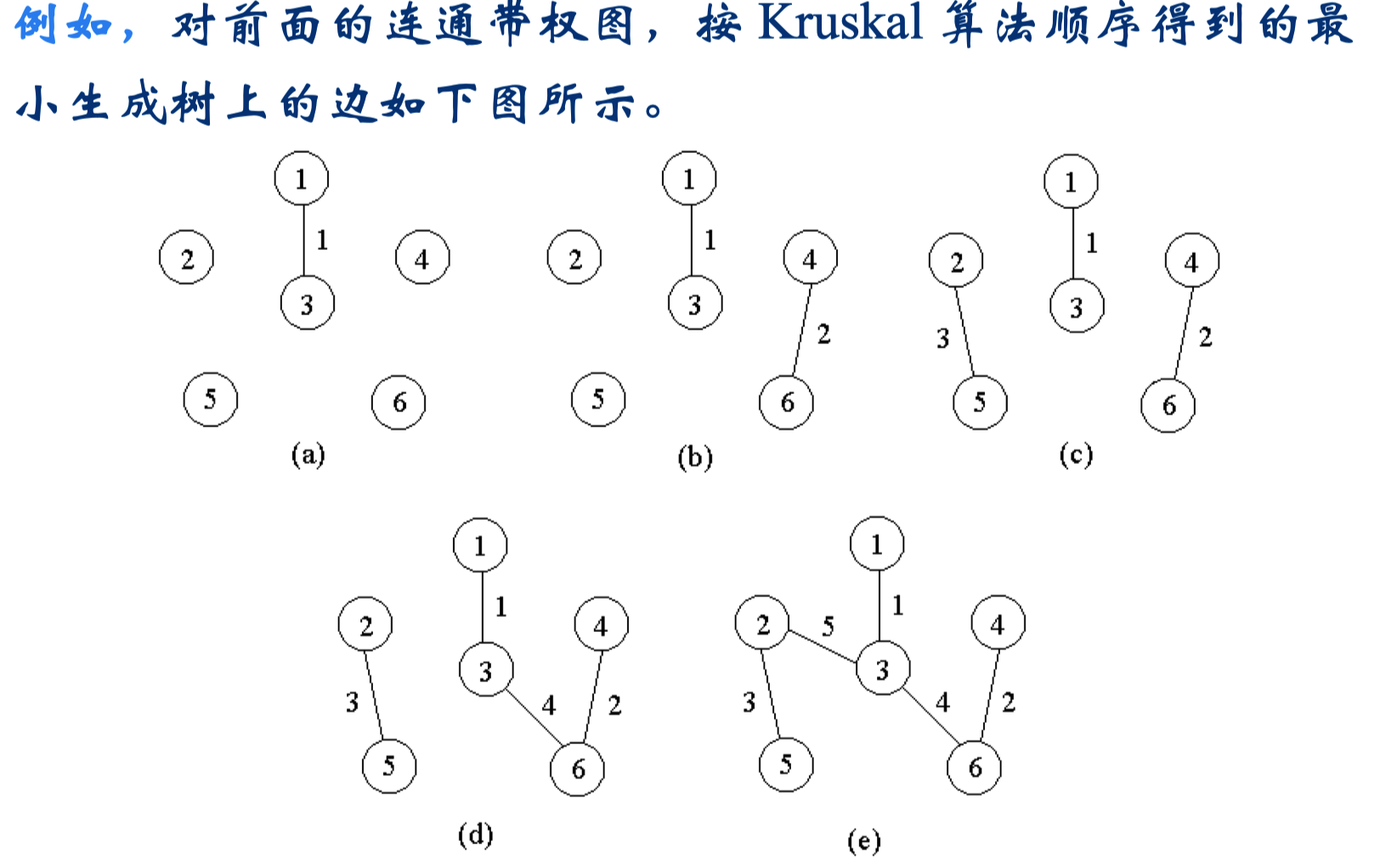
(2)Kruskal 算法
Kruskal算法构造 G 的最小生成树的基本思想:
- 首先将 G 的 n 个顶点看成 n 个孤立的连通分支,将所有的边按权从小到大排序
- 从第一条边开始,依边权递增的顺序查看每一条边,并按下述方法连接 2 个不同的连通分支:
- 当查看到第 $k$ 条边 $(v,w)$ 时,如果端点 $v$ 和 $w$ 分别是当前 2 个不同的连通分支 $T_1$ 和 $T_2$ 中的顶点时,就用边 $(v,w)$ 将 $T_1$ 和 $T_2$ 连接成一个连通分支,然后继续查看第 $k+1$ 条边
- 如果端点 $v$ 和 $w$ 在当前的同一个连通分支中,就直接再查看第 $k+1$ 条边
- 这个过程一直进行到只剩下一个连通分支时为止
- 当图的顶点数为 $n$,边数为 $e$ 时,Kruskal算法所需的计算时间是 $O(e \log{e})$
4.7 多机调度问题

这个问题是 NP完全问题,到目前为止还没有有效的解法, 对于这一类问题,用贪心选择策略有时可以设计出较好的近似算法。
贪心策略:最长处理时间作业优先。
- 当 $n \leq m$ 时,只要将机器 $i$ 的 $[0, t_i]$ 时间区间分配给作业 $i$ 即可,算法只需要 $O(1)$ 时间
- 当 $n \gt m$ 时,首先将 $n$ 个作业依其所需的处理时间从大到小排序;然后依此顺序将作业分配给空闲的机器处理。
- 算法所需的时间复杂度为 $O(n \log{n})$

4.7 会场安排问题


(1)贪心策略:
在满足与前一个活动相容的情况下,优先选择开始时间早的活动。
(2)最优子结构
设原问题为$E$的最优解为$A$,现在假设活动1为会场1中安排的第一个活动。那么,可以得到与活动1相容的子问题$E’=E-{1}$,现在需要证明$A’=A-{1}$是$E’$的最优解。
反证:假设存在子问题$E’=E-{1}$的一个最优解为$A’’$,那么有$|A’’|<|A’|$,即$|A’’ \cup {1}|<|A’ \cup {1}|=|A|$,与$A$是原问题$E$的最优解矛盾。
(3) 贪心选择性质
现在假设最优解$E$,按照活动的开始时间非减序排列${s_1,s_2,\dots,s_n}$,对应的结束时间为${f_1,f_2,\dots,f_n}$。
设在满足会场1相容条件(即开始时间大于会场1前一个活动结束时间)的前提下,第一个安排到会场1中的活动为$a_1$,而开始时间最早的活动为$a_k$。
- 若 $k=1$,即为满足贪心选择性质的最优解。
- 若$k \neq 1$,因为$s_k<s_1$,所以它们一定不会安排在同一个会场。假设活动$a_k$安排在第$m$个会场,会场$m$前一个活动为$a_x$,即有$s_k \geq f_x $。现在将$a_1$与$a_k$的会场进行互换得到解$E’$,因为$a_1$与$a_k$均满足会场1的相同条件,且$s_1 \gt s_k \geq f_x$,即$a_1$也满足会场$m$的相容条件,所以$E’$为该问题的一个可行解。又因为$|E’|=|E|$,所以$E’$是满足贪心选择性质的最优解。
(4)代码:
1 | /* |
4.8 最优合并问题

(1)贪心策略
- 最优合并策略:优先序列长度最小的两个序列进行合并。
- 最差合并策略:优先序列长度最大的两个序列进行合并。
(2)贪心选择策略
与哈夫曼编码问题等价,设$S$为要合并的序列集合,其中$S_i,S_j$具有最小的序列长度,则存在$S$的最优合并二叉树$T$,使得$S_i$和$S_j$为$T$中最深叶子结点且为兄弟结点。
证明:
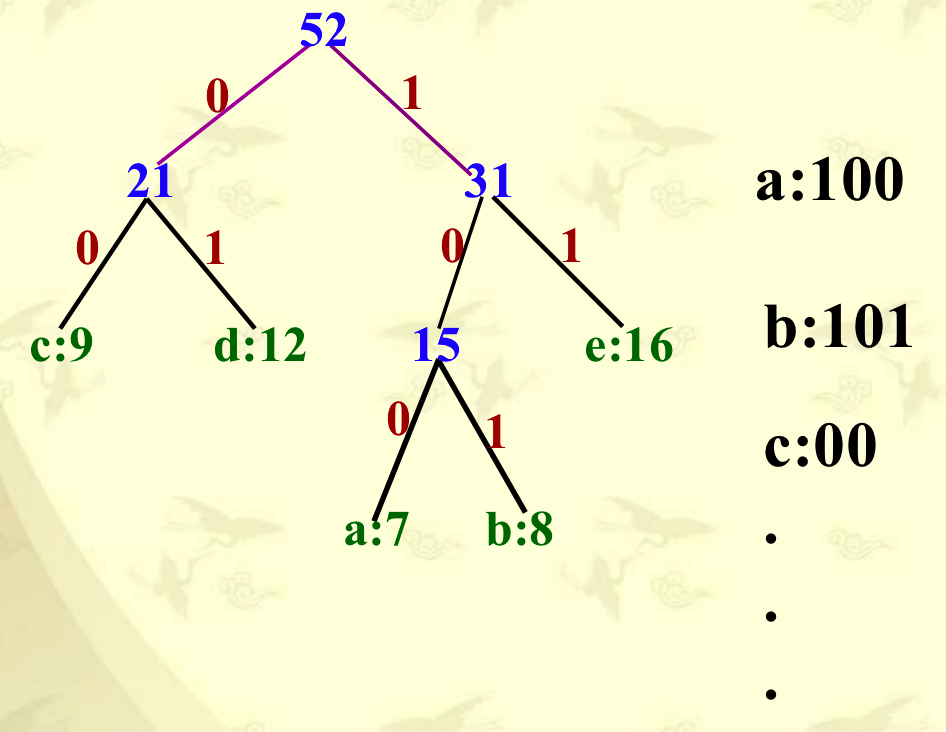
假设$S$中的任意两个序列$S_m,S_n$为二叉树$T$的最深叶子且为兄弟。不是一般性,可设$S_m<S_n$,$S_i<S_j$。因为$S_i,S_j$具有最短的序列长度,所以$S_i \leq S_m$,$S_j \leq S_n$。如下图,对二叉树$T$交换叶子$S_m$和$S_i$的位置得到二叉树$T’$,再对$T’$交换$S_n$和$S_j$的位置得到二叉树$T’’$。
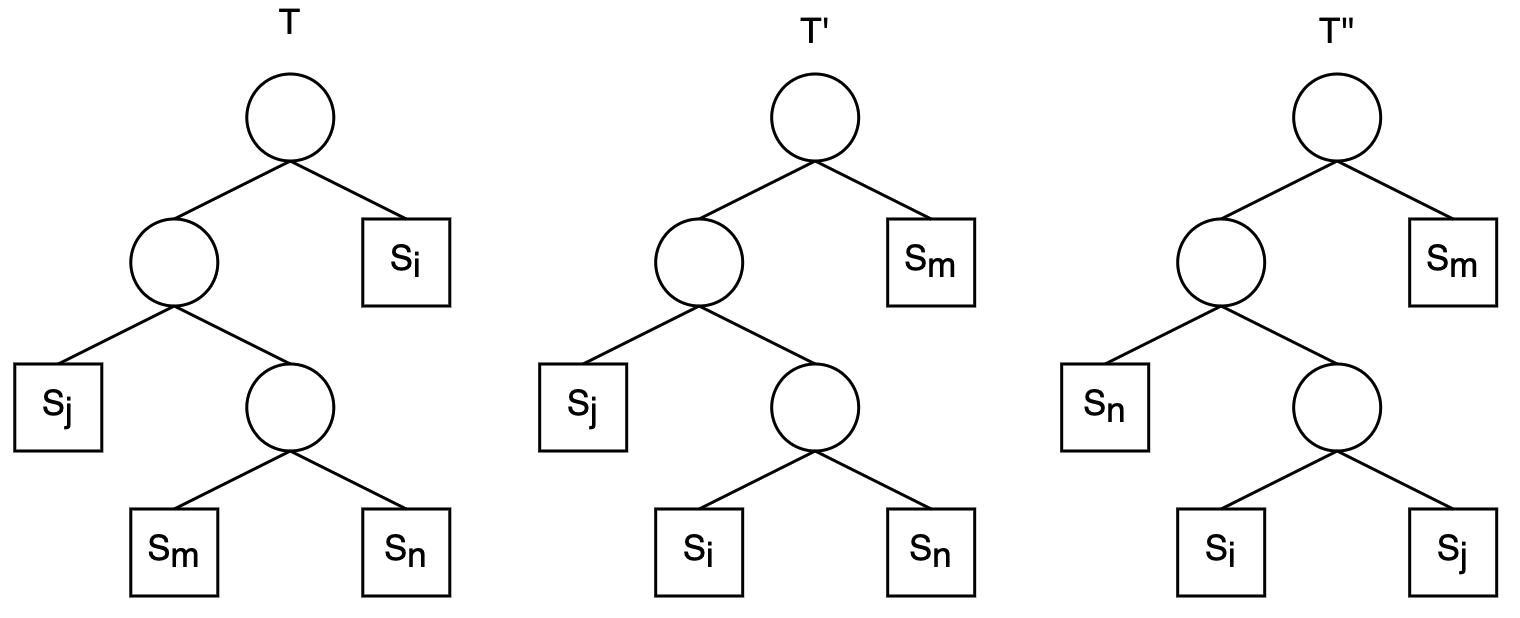
设合并二叉树$T$所需比较次数用$B(T)$表示,则有:
$$
B(T) = (S_m+S_n-1)+(S_j+S_m+S_n-1)+(S_j+S_m+S_n+S_i-1)\
B(T’)= (S_i+S_n-1)+(S_j+S_i+S_n-1)+(S_j+S_i+S_n+S_m-1)\
B(T)-b(T’)=2(S_m - S_i) \geq 0
$$
同理可得,$B(T’)-B(T’’) \geq 0$,因此有$B(T) \geq B(T’) \geq B(T’’)$,即$T’’$表示合并二叉树为最优的 ,此时序列长度最短的两个序列$S_i,S_j$为最深叶子结点且为兄弟。
(3)最优子结构
设原问题的最优合并二叉树为$T$,$S_i,S_j$是二叉合并树$T$的叶子结点且为兄弟,$Z=S_i+S_j$是它们的父亲结点,则树$T’=T-{S_1,S_2}$是子问题$S’=S-{S_1,S_2} \cup {Z}$的最优合并二叉树。
反证:
若子问题$S’$存在一个更优的合并二叉树$T’’$,即$B(T’’) \lt B(T’)$ ,那么将会有$B(T’’-{Z} \cup {S_1,S_2}) \lt B(T’-{Z} \cup {S_1,S_2})=B(T)$,与$T$是原问题的最优解矛盾。
(4)时间复杂度
实现上可以通过优先级队列,主要的复杂度来自于队列的排序过程,即$O(nlogn)$
(5)代码:
1 | /* |
4.9 汽车加油问题

(1)贪心策略
如果当前汽车的油足够行驶到下一个加油站,则不加油,否则加油,即让汽车行驶尽可能远的距离再加油。
(2)贪心选择性质
设汽车在加满油行驶的$n$千米内任取两个加油站$X$和$Y$,且它们距起点的距离分别为$x$千米和$y$千米($x \lt y$)。那么,若汽车在加油站$Y$加油不足以到达终点,那么其在加油站$X$加油也必然不能到达终点,因为$x+n \lt y+n$,而在$Y$加油比在$X$加油可以多行驶$y-n$千米。为了使加油次数尽可能的少,据需要使汽车每次加完油都行驶尽可能远的距离。
(3)最优子结构
设原问题的最优解为$A[1:k]$,表示从起点(第$0$个加油站)到终点(第$k+1$个加油站)汽车加油问题。若在第$i$个加油站进行加油,那么总共的加油次数就等于子问题$A[1:i]$的加油次数,加上子问题$A[i+1:k]$的加油次数,再加上$1$,并且$A[1:i]$和$A[i+1:k]$均具有最优子结构。
反证:如果存在更优的加油位置$i’$使$A[1:i’]$或$A[i’+1:k]$的存在更优的解,那么用它替换$A[1:i]$或$A[i+1:k]$得到的$A[1:k]$计算量也会比定义的最优解次数更少,导致矛盾。
(4)代码
1 | /* |
(5)时间复杂度
只需要一次循环即可得到答案,时间复杂度为$O(n)$。
4.10 磁盘文件最优存储问题


(1)贪心策略
优先将检索概率大的文件存储在磁盘的中间磁道上。
具体的,假设针对文件${f_1,f_2,\dots,f_n}$按检索概率非增序排列,那么首先将$f_1$放在中间磁道($n/2$)上,然后将$f_2$和$f_3$分别存放到$f_1$的左右两侧磁道,再将$f_4$存放在$f_2$的旁边,$f_5$存放在$f_3$的旁边, 以此类推。
(2)正确性证明
对于期望时间$\sum p_i p_j d(i,j)$ ,$p_i p_j$是根据输入固定的,我们能优化的为$d(i,j)$,因此对于更大的$p_i p_j$希望其能够具有更小的$d(i,j)$,即概率大的两个磁道尽量靠近。
假设$n$文件中检索概率最大的三个文件分别为$f_i,f_j,f_k (p_i > p_j > p_k)$,设$D_{ijk},D_{jik},D_{jki}$分别表示将概率检索概率最大的文件$f_i$分别放在最左侧,中间和最右侧时的检索时间,可以得到:
$$
D_{ijk}=p_i p_j d + p_i p_k 2d + p_j p_k d \
D_{jik}=p_j p_i d + p_j p_k 2d + p_i p_k d \
D_{jki}=p_j p_k d + p_j p_i 2d + p_k p_i d \
D_{jik}-D_{ijk}=p_j p_k d - p_i p_k d=(p_j -p_i)p_k d < 0 \
D_{jik}-D_{jki}=p_j p_k d - p_j p_i d = (p_k - p_i) p_j d < 0 \
$$
得到$D_{jik}<D_{ijk},D_{jik}<D_{jki}$,也就是将检索概率最大的文件$f_i$存放在磁道中间位置具有更小的检索时间,满足贪心选择策略。
(3)代码
1 | /* |
(4)时间复杂度
对检索概率排序需要$O(nlogn)$,将文件存放到磁道上需要$O(n)$,计算期望检索时间需要$O(n^2)$.
5 回溯法
回溯法的主要思想为深度优先搜索。
解向量:回溯法希望一个问题的解能够表示成一个 $n$ 元式 $(x_1 ,x_2, \dots, x_n)$ 的形式
常用剪枝函数:
- 用约束函数在扩展结点处剪去不满足约束的子树
- 用限界函数剪去得不到最优解的子树
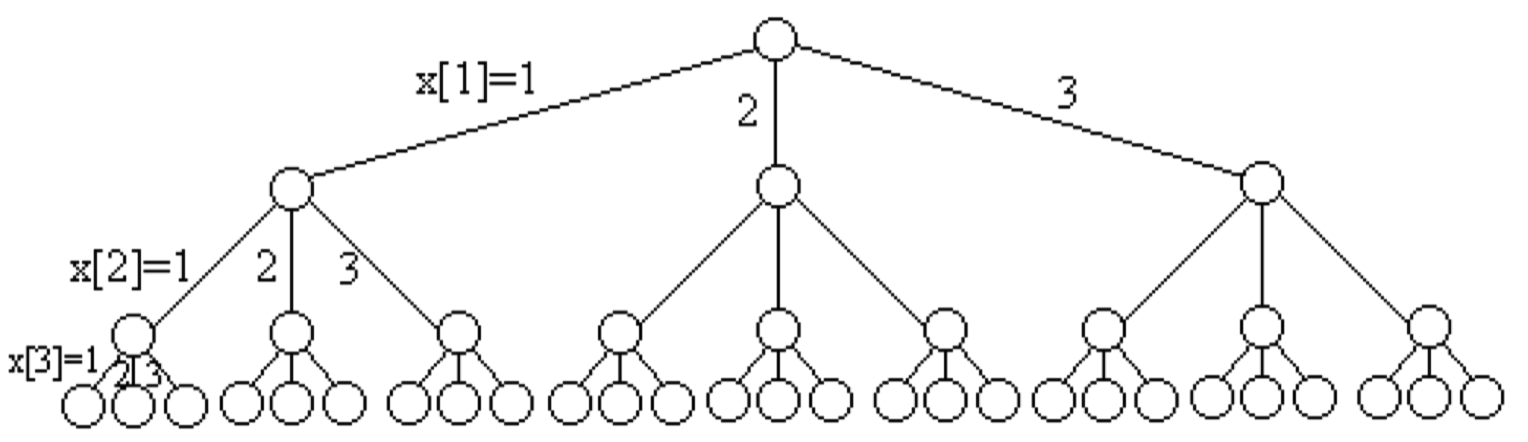
解空间:子集树与排列树
<img src=”data:image/svg+xml,“ alt=”image-20220526114359851” style=”zoom:40%;” />
5.1 装载问题
问题同4.2,有一批共 $n$ 个集装箱要装上 2 艘载重量分别为 $c_1$ 和 $c_2$ 的轮船, 其中集装箱 $i$ 的重量为 $w_i$ ,且 $\sum_{i=1}^{n} w_i \leq c_1 + c_2$。装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这 2 艘轮船;如果有,找出一种装载方案?
思路:容易证明,如果一个给定装载问题有解,则采用下面的策略可得到最优装载方案:先将第一艘轮船尽可能装满,然后将剩余的集装箱装上第二艘轮船。将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集, 使该子集中集装箱重量之和最接近 $c_1$。
解空间:子集树。
左儿子表示选择装入当前集装箱,需要判断可行性;右儿子表示不选择装入当前集装箱,总是可行的,但是通过限界函数判断其子树是否存在更优解,不存在则剪去。
可行性约束函数:选择当前元素后,选择装入的集装箱总重量不超过轮船载重量,$\sum_{i=1}^{n}w_ix_i \leq c_1$。
限界函数:当前载重量 $\text{cw}$ + 剩余集装箱的重量 $\text{r}$ $\leq$ 当前最优载重量$\text{bestw}$,也就是 $cw + r \leq bestw$ 时,可以剪去右子树。
搜索过程:
5.2 批处理作业调度

解空间:排列树
优化目标:所有作业在机器2上完成的时间和最小 $\min{\sum_{i=1}^{n}F_{2i}}$
搜索过程:
- 当 $i>n$ 时,算法搜索至叶子结点,得到一个新的作业调度方案。此时算法适时更新当前最优值和相应的当前最佳调度。
- 当 $i<n$ 时,当前扩展结点位于排列树的第 $(i-1)$ 层,此时算法选择下一个要安排的作业,以深度优先方式递归的对相应的子树进行搜索,对不满足上界约束的结点,则剪去相应的子树。
- 上界约束,当前在机器二上的完成时间和已经会超过当前最优解,即该子树不存在更优解。
- 处理作业 $i$ 时,比较 $i$ 在机器1上的结束时间,和作业 $i-1$ 在机器2上的结束时间,较大的那个作为第 $i$ 个任务在机器2上的开始时间。
- 最坏情况下复杂度 $O(n!)$

5.3 符号三角形

解空间:子集树。用 n 元组 $x[1:n]$ 表示符号三角形的第一行,每个元素选择
+或-。可行性约束函数:当前符号三角形所包含的 “+” 个 “-” 个数均不超过 $n(n+1)/4$
最坏情况时间复杂度 $O(n 2^n)$
5.4 n 后问题

解空间:排列树,解向量为 $x[1:n]$ 的排列,其中 $x[i]$ 表示皇后 $i$ 放在棋盘的第 $i$ 行的第 $x[i]$ 列。
可行性约束函数:显然各皇后不在同一行,还需要不在同一列($x[i] \neq x[j]$),以及不在同一对角线($|i-j| \neq |x_i - x_j|$)。
搜索过程:当 $i>n$,到达叶结点,得到n后问题的一个可行解。当 $i\leq n$时,对当前扩展结点的每个儿子结点进行可行性的检查,并以深度优先的方式递归地对可行子树进行搜索,或剪去不可行子树,
5.5 0-1背包问题
解空间:子集树。
每一个扩展结点左儿子表示当前物品装入背包,符合可行性约束才进入左子树;右儿子表示不装入背包,只有存在更优解时才进入右子树。
可行性约束函数:当前装入物品的总重量不超过背包容量,即 $\sum_{i=1}^{n}w_ix_i \leq c$
上界函数:当前子树所具有的总价值,不会超过当前最优解,即 $\sum_{j=1}^{i}w_iv_i + r \leq bestp$
计算更好的上界的方法是:将剩余物品根据单位重量价值排序,然后依次装入物品,直到装不下时,再装入该物品的一部分而装满背包,此时得到的价值是右子树中解的上界。

5.6 最大团问题
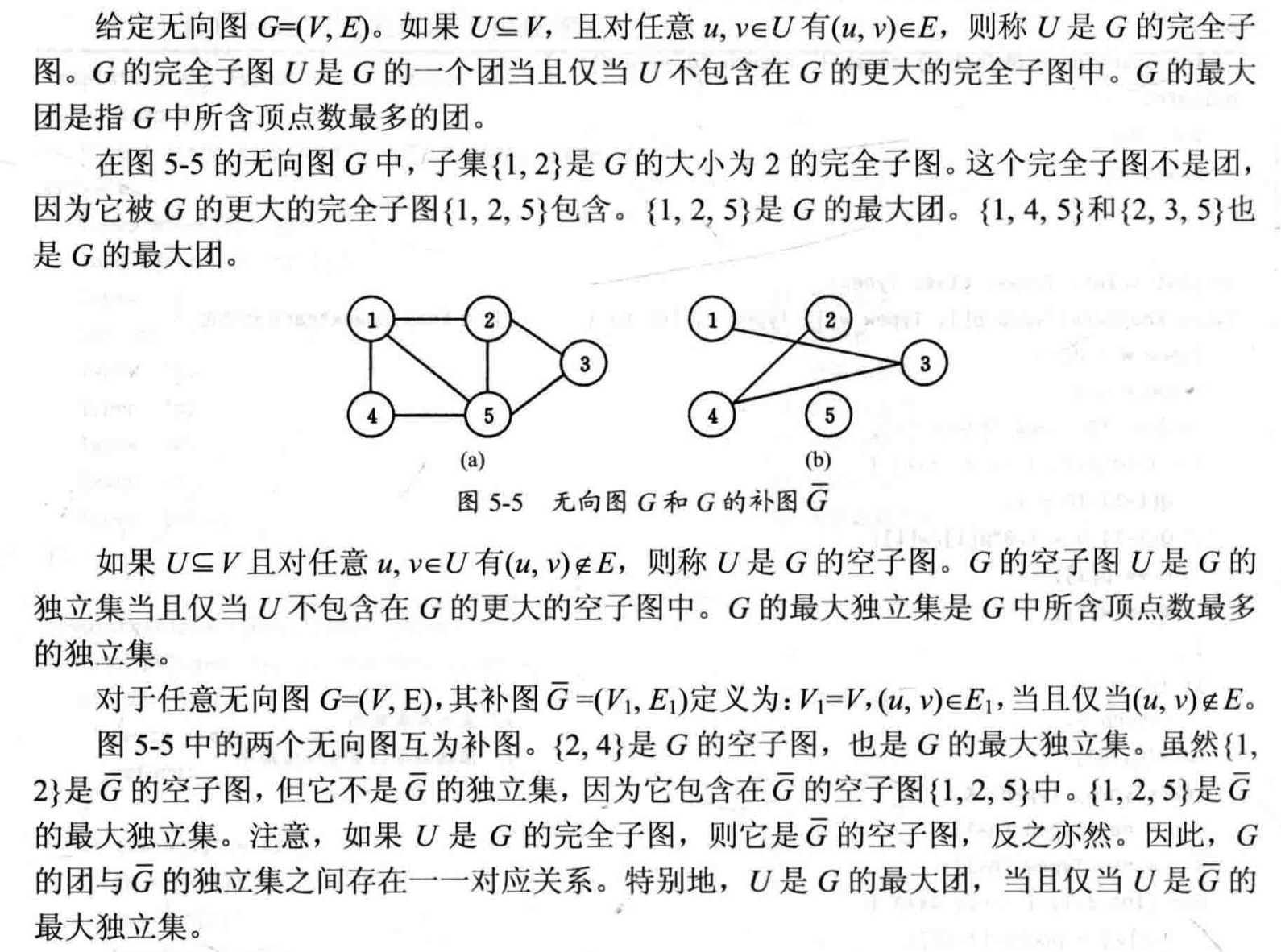
- 解空间:子集树
- 可行性约束函数:顶点 $i$ 到已选入顶点集中每一个顶点都有边相连
- 上界函数:有足够多的可选择顶点 使得算法有可能在右子树中找到更大的团
- 搜索过程:设当前扩展结点 $Z$ 位于解空间树的第 $i$ 层,进入左子树前,先确认从顶点 $i$ 到已选入的顶点集中每个顶点都有边相连;进入右子树前,先确认还有足够多的可选择顶点,使算法有可能在右子树中找到更大的团。
- 复杂度 $O(n 2^n)$
5.7 图的m着色问题
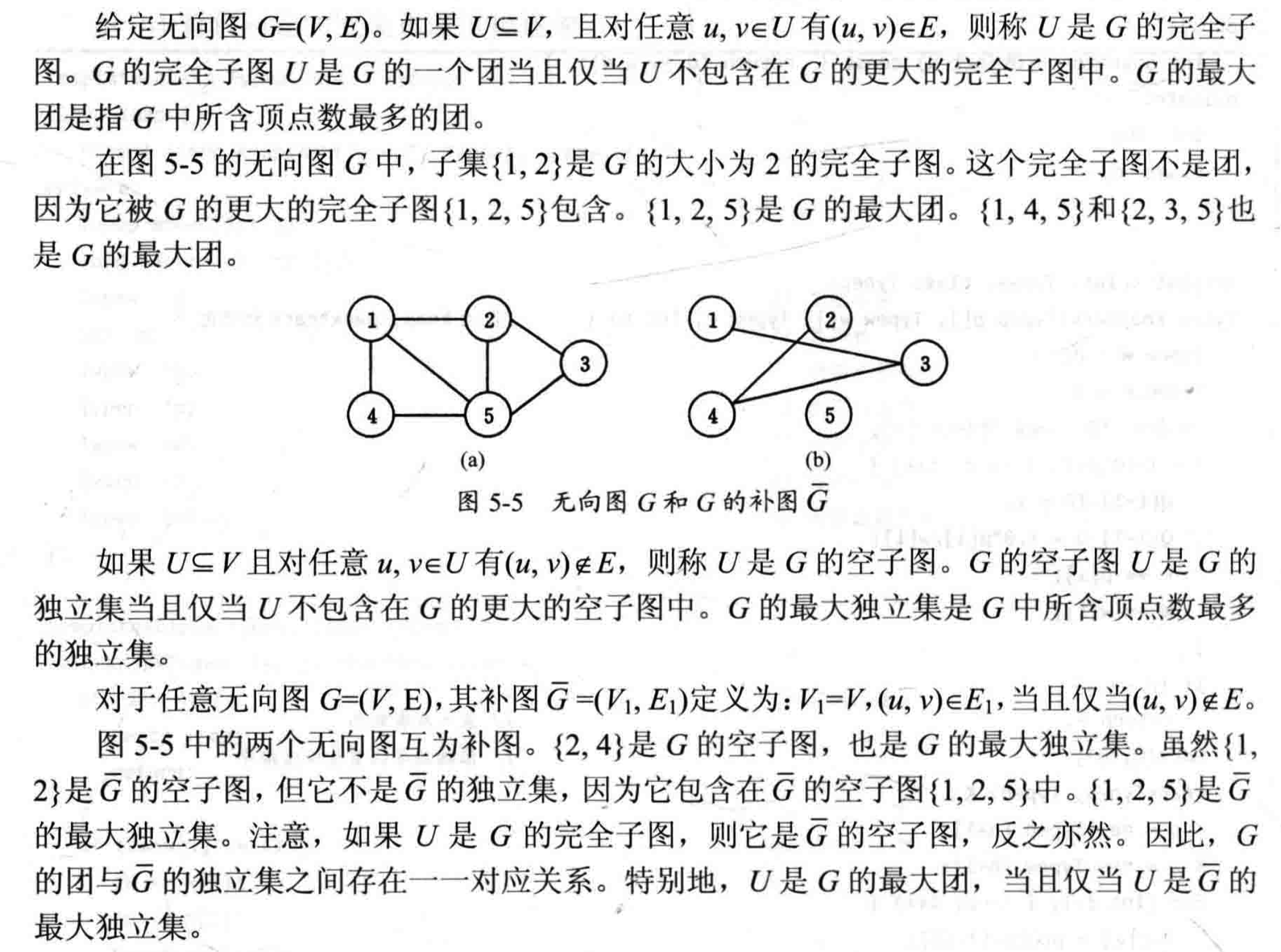
解空间:排列树,是一个 $n+1$ 层的完全 $m$ 叉树。用$x[1:n]$ 表示解向量,其中 $x[i]$ 表示顶点 $i$ 所着颜色为 $x[i]$,第 $i$ 层中每个结点有$m$个儿子,每个儿子对应于 $x[i]$ 的 $m$ 个可能的着色之一。
可行性约束函数:顶点 $i$ 与已着色的相邻顶点颜色不重复
搜索过程:
- 当 $i > n$ 时,算法搜索到叶结点,此时得到一个新的着色方案。
- 当 $i \leq n$ 时,当前扩展结点$Z$ 有 $m$ 个儿子结点 $x[i]$。对当前扩展结点 $Z$ 的每个儿子结点,用可行性约束函数判断其可行性,并以深度优先的方式递归地对可行子树进行搜索,或剪去不可行子树。
5.8 旅行售货员问题

- 解空间:排列树,解向量为 $x[1:n]$ 的所有排列。
- 可行性约束函数:是否存在一条从顶点 $x[i-1]$ 到顶点 $x[i]$ 的边,即是否存在相连路径;如果 $i=n$ 则还需要判断师傅和一条从顶点 $x[n]$ 到 顶点 1的边,即是否构成一个回路。
- 上界约束函数:当前已走过路径的费用是否优于已找到的当前最优回路费用 bestc。
- 搜索过程:
- 当 $i=n$ 时,当前扩展结点时排列树叶结点的父结点。此时,通过可行性约束判断当前路线是否存在一条满足要求的回路,若存在,则得到一个可行解。然后判断,该可行解的费用是否优于当前已找到的最优路线费用。如果是,则更新当前最优值和最优解。
- 当 $i < n$ 时,当前扩展结点位于排列树的第 $i-1$ 层。用可行性约束判断图 $G$ 中是否存在从顶点 $x[i-1]$ 到顶点 $x[i]$ 的边,$x[1:i]$ 构成图G的一条路径,且当 $x[1:i]$ 的费用小于当前最优值时算法进入排列树的第 $i$ 层,否则剪去相应的子树。
5.9 连续邮资问题

- 解向量:用 $n$ 元组 $x[1:n]$ 表示 $n$ 种不同的邮票面值,约定它们从小到大排列。$x[1]=1$ 是唯一的选择,因为要贴出1的邮资。
- 可行性约束函数:已选定 $x[1:i-1]$,最大连续邮资区间是 $[1:r]$,接下来 $x[i]$ 的可取值范围是 $[x[i-1]+1:r+1]$

5.10 最小电路板长度排列问题

该问题的解空间是一个排列树。当$i=n$到达叶节点时,所有电路板已排列,遍历每一个连接块,并对每一个连接块都分别从排列的左侧和右侧对电路板进行编列,从而找到该连接块的长度。我们记录所有连接块中的最大长度,并比较它与当前最优值的大小,如果小于当前最优值,则对最优值和最优解进行更新。
代码:
1 |
|
5.11 无和集问题

解空间为一棵子集树,树的每一层表示一个子集。
可行性条件:对于一个已有的递增子集,现在要判断新增的数能否加入该子集中。如果通过判断“任意两个数的和不在该子集中”,那么就需要双重循环遍历进行判断。因此,可以转换一下思路,让新增的数与子集中每一个数做减法,若如果它们的差值也存在于该子集中,则说明该数不能插入该集合中,这种方法只需要一次循环即可判断。
思路:
对于每一个新增的数,首先进行可行性的判断,判断其是否能加入到当前层所表示的子集中:
- 如果不能插入当前层表示的子集,就继续判断该新增的数其能否插入到下一层所表示子集中。
- 如果可以插入当前层表示的子集,那么就存在两个儿子节点,分别为插入当前子集和不插入当前子集。
- 如果选择插入当前子集,则从第一层开始再将判断下一个新增的数。
- 如果选择不插入当前子集,则继续判断是否将该数插入下一个子集。
代码:
1 | // 无和集问题 |
5.12 工作分配问题

解空间为一个经典的排列树,得到最优解为x[n],表示将第i个工作分配给第x[i]个人去做,在到达叶节点得到一个排列后,只需要根据当前排列查询每个工作i的所需的费用c[i][x[i]]进行累加,即可得到总费用。如果总费用小于最优值,则更新当前最优值和最优解。
代码:
1 |
|
5.13 拉丁矩阵问题

共有n种宝石,排列成m*n的矩阵,因此每一行均为$n$种组成的排列,解空间为排列树。对矩阵的每一行进行全排列,同时满足可行性条件,即该行与之前所有行的每一列没有形状重复的宝石。
因此,用函数ok(r,c)判断第c列的前r行是否存在重复的宝石,回溯方法traceback(r,c)对每一行进行排列,使用排列树的框架,没有优化目标,找出所有可行解即可,当搜索到最后一行最后一列时,可行解的数量加一。
代码:
1 | /* |
6 分支限界法
求解目标不同
- 回溯法找出解空间中满足约束条件的所有解。
- 分支限界法找出满足约束条件的一个解,或是在满足约束条件的解中找出某种意义下的最优解
搜索方式不同
- 回溯法:深度优先搜索
- 分支限界法:广度优先搜索或最小耗费(最大效益)优先
活结点扩展方式
- 分支限界法中每一个活结点只有一次机会成为扩展结点,活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。此后,从活结点表中取下一结点成为当前扩展结点,重复上述结点扩展过程,一直持续到找到所需的解或 活结点表为空时为止。
- 回溯法中的结点有可能多次成为活结点。
(2)常用的两种分支限界法
- 队列式 (FIFO) 分支限界法
- 按照队列先进先出(FIFO)原则选取下一个节点为扩展节点
- 优先队列式分支限界法
- 按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点
- 在搜索解空间过程中增加了启发式方法,并通过优先级数值体现
6.1 单源最短路径问题
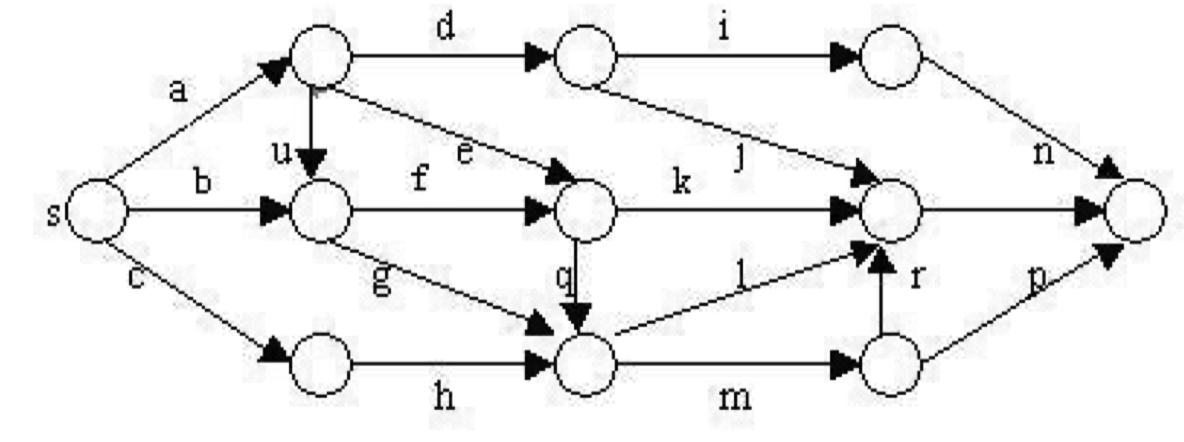
以当前结点的路径长度作为优先级建立最小堆,从而实现活结点的优先级队列。
算法从图 G 的源顶点 s 和空优先队列开始,结点 s 被扩展后,它的儿子结点被依次插入堆中
从活结点列表中取出具有最小当前路径长度的结点作为当前扩展结点,并依次检查与当前扩展结点相邻的所有顶点:
- 如果从当前扩展结点 i 到顶点 j 有边可达(可行性约束)
- 从源出发,途经顶点 i 再到顶点 j 的所相应的路径的长度小于当前最优路径长度(上界约束),否则剪去改结点为根的子树。
- 则将该顶点作为活结点插入到活结点优先队列中
结点的扩展过程一直继续到活结点优先队列为空时为止
6.2 装载问题
解空间为子集树,节点的左子树表示将此集装箱装上船,右子树表示不将此 集装箱装上船。
(1)基于队列的分支限界
- 检测当前扩展结点的左儿子是否为可行结点(可行性约束,即不超过轮船载重量),如果是则加入到活结点列表中。
- 将其右儿子结点加入到活结点队列中 ,右儿子结点一定是可行结点,但是需要用限界函数判断是否存在更优解。
- 设 bestw 是当前最优解,ew 是当前扩展结点所相应的重量,r 是剩 余集装箱的重量
- 则当 ew+r $\leq$ bestw 时,可将其右子树剪去,因为此时若要船装最多z集装箱,就应该把此箱装上船
- 另外,为了确保右子树成功剪枝,应该在算法每一次进入左子树的 时候更新 bestw 的值
(2)基于优先级队列的分支限界
- 用最大优先队列存储活结点表
- 活结点 x 在优先队列中的优先级定义为从根结点到结点 x 的路径所相应的载重量再加上剩余集装箱的重量之和
- 优先队列中优先级最大的活结点成为下一个扩展结点
- 以结点 x 为根的子树中所有结点相应的路径的载重量不超过它的优先级
- 子集树中叶结点所相应的载重量与其优先级相同
- 优先队列式分支限界的终结
- 一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解,此时可终止算法
6.3 布线问题
FIFO队列式分支限界法:
- 从起始位置 a 开始将它作为第一个扩展结点
- 与扩展结点相邻并且可达的方格成为可行结点(可行性约束),将其加入到活结点队列中,并且将这些方格标记为 1。
- 算法从活结点队列中取出队首元素作为下一个扩展结点,并将与 当前扩展结点相邻且未标记过的方格标记为 2,并存入活结点队列。
- 一直继续到算法搜索到目标方格 b 或活结点队列为空
6.4 0-1背包问题
要对输入数据进行预处理,将各物品依其单位重量价值从大到小进行排列
优先级队列分支限界法:
优先级定义为:“已装入的物品价值”加上“剩下最大单位重量价值的物品装满剩余容量”的价值和,也就是当前结点可能装入背包的价值上限。
可行性约束:装入该物品后的重量是否超过背包总容量
上界约束:当前已装入的物品价值加上用剩余最大单位重量价值的物品装满剩余容量的价值和,是否超过当前最优价值(因为已经按单位价值排序,因此直接按顺序装满背包即可)。
首先,检查当前扩展结点的左儿子是否满足可行性约束,如果左儿子是可行结点,则将其加入到活结点优先队列中。
当前扩展解的右儿子一定是可行结点,仅当右儿子结点满足上界约束时,才将其加入到子集树和活结点优先队列中。
不断从活结点列表中取出队首元素作为扩展结点,直到到达叶结点得到问题的最优值。
6.5 旅行售货员问题
某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费),他要选定一条从驻地出发,经过每个城市一 次,最后回到驻地的路线,使总的路程(或总旅费)最小。
解空间为排列树,排列树,解向量为 $x[1:n]$ 的所有排列。
优先级定义从源结点到当前结点路程所需的费用加上当前扩展结点最小出边费用,用最小堆实现。
可行性约束:对于当前扩展结点 $i$,是否存在一条从顶点 $x[i-1]$ 到顶点 $x[i]$ 的边,即是否存在相连路径;如果 $i=n$ 则还需要判断师傅和一条从顶点 $x[n]$ 到 顶点 1的边,即是否构成一个回路。
上界约束函数:当前已走过路径的费用加上当前扩展结点最小出边费用,是否优于已找到的当前最优回路费用 bestc。
搜索过程:
当 $s=n-2$,即当前扩展结点时排列树中某个叶结点的父结点。判断该叶结点是否可以构成一条可行回路(满足可行性约束),并且费用小于当前最小费用(满足界限约束),则将该叶结点 插入优先队列中,否则舍去该叶结点。
当 $s \lt n-2$,产生当前扩展结点的所有儿子结点,对于每一个儿子结点,判断是否满足可行性约束(即与剩下的顶点存在相连的边)。对于每一个可行的儿子结点,再判断其是否满足界限约束(当前扩展结点的每个儿子结点,计算出其路径所需的费用加上该儿子结点最小出边的费用),若小于最优解,则将该可行儿子结点加入到活结点优先队列中。
while循环的终止:条件是排列树的一个叶结点成为当前扩展结点,当 $s=n-1$ 时,已找到的回路前缀是 $x[0:n-1]$,已包含所有 $n$ 个顶点。当 $s=n-1$ 时,相应的扩展结点表示叶结点,剩余活结点不小于已找到回路的费用,算法终止。
6.6 0-1背包问题的栈式分支限界

首先根据物品的单位价值进行进行非升序排列。算法不断扩展结点,首先检查当前扩展结点的左儿子是否为可行结点,可行性约束为已入背包的重量加上该结点重量后是否超过背包总重量,如果左儿子是可行结点,则将其加入到活结点栈中。当前扩展结点的右儿子一定是可行结点,判断其是否符合上界约束,即其所包含的子数存在更优解时才将其加入到活结点栈中。
分支限界法与回溯法的区别在于,分支限界法中每一个活结点只有一次机会,且活结点一旦成为扩展结点,就一次性产生其所有儿子结点。此后,从活结点表中取下一结点作为当前扩展结点,直到找到所需的解或活结点表为空,其主要思想为广度遍历优先。而回溯法中的结点有可能多次成为活结点,其主要思想为深度遍历优先。
6.7 最小长度电路板排列问题

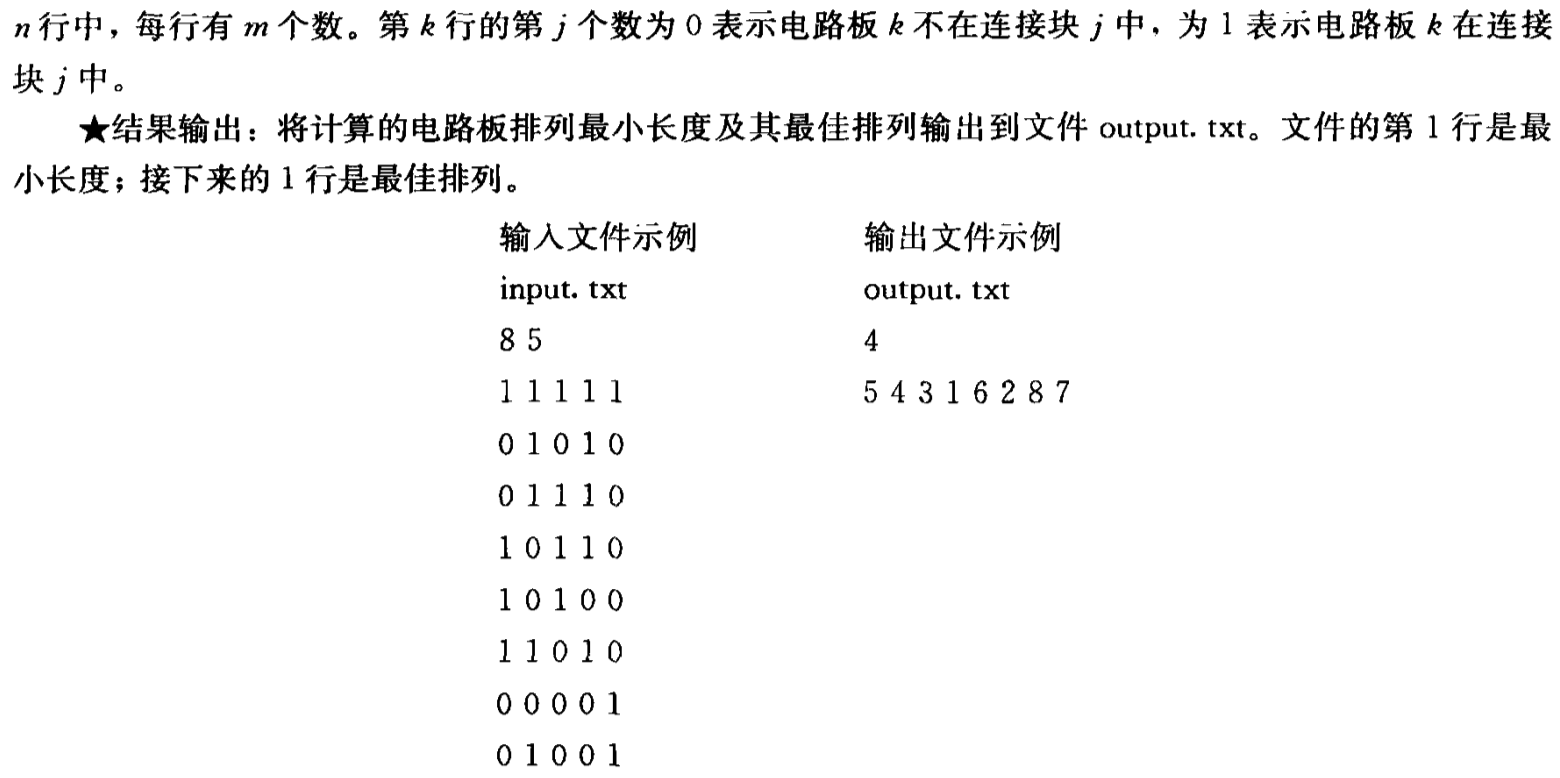
该问题的解空间是一颗排列树,用 BoardNode类表示排列树的每个结点,其中包含 x 表示相应结点的电路板排列,s 表示该结点已确定的电路板排列x[1:s],cd表示当前的长度,数组low和high分别表示每个连接块第一个和最后一个电路板的位置,当需要计算当前排列的最小长度是,只要依次将high和low中的元素做减法,并取其中最小值即可。
当使用队列式分支限界法时,依次对排列树内部结点进行扩展,当s=n-1时,已排定n-1块电路板,当前扩展结点是排列树中叶结点的父结点,x表示相应于该叶结点的电路板排列,计算出此时x的长度,若小于当前的最优值,则更新最优值和最优解。当s<n-1时,算法依次产生当前扩展结点的所有儿子结点。对于每一个儿子结点,计算出其长度,若小于当前的最优值,则将该儿子结点插入到活结点队列中,否则舍去该儿子结点。do-while循环依次从活结点队列中取出结点作为当前扩展结点,直到队列为空时,算法结束。
当使用优先级队列分支限界法时,用当前结点的长度cd作为优先级插入优先级队列中(最小堆)。do-while循环依次从活结点优先级队列中取出结点作为当前扩展结点,如果当前扩展结点的长度cd不小于当前最小长度,则优先级毒烈中其余活结点都不可能导致最优解,算法结束。
6.8 最小权顶点覆盖问题

该问题的解空间是一个子集树,以当前扩展结点的权重作为优先级建立最小堆,从而实现活结点优先级队列。
设组成顶点覆盖的集合为
U,约束条件为集合U中的点集能够完成对图G的顶点覆盖。具体做法可以每个活结点开辟一个数组c,每次将顶点i加入到集合U时,依次判断n个顶点是否与i有相连的边,如果顶点j与顶点i有边,则将c[j]加一,若最终c[j]=0,则说明当前U并没有覆盖到顶点j。利用数组c,可以判断当前扩展结点是否完成顶点覆盖,即遍历所有顶点j(1<=j<=n),若j既不是U中的点(E.x[j]=0),也没有与U中的顶点相连(E.c[j]=0),则说明未完成顶点覆盖。当
i>n时,到达叶结点,判断当前最优解是否完成了顶点覆盖,若已完成则更新最优值和最优解。当
i<n时,对于当前扩展结点,如果没有完成顶点覆盖,才有必要将左儿子加入到活结点队列中,否则无需选择左儿子来进一步增加集合U中的权重;该问题无法设定界限约束,右儿子则直接加入到活结点队列中,因为如果只选择右儿子,那么覆盖集顶点权重一定更小,但是却不一定能够完成顶点覆盖
代码:
1 | // 最小权顶点覆盖问题 |
最小堆MinHeap.h的代码如下:
1 | template <class Type> |
6.9 最小重量机器设计问题

解空间为深度为n的m叉树。
解空间树的第 i 层表示第 i 个物品,每一层有 m 个结点,分表表示对应的供应商,用数组 best_x[n] 表示最优解,其中 bestx[i] 表示第 i 个物品从第 bestx[i] 个供应商采购。
以当前扩展结点的重量作为优先级建立最小堆,从而实现活结点优先级队列。
当活结点队列不为空时,依次从中取出扩展结点,如果未到达叶结点,则遍历当前扩展结点的所有儿子结点(即遍历所有供应商)。
- 如果儿子结点为叶结点,每次遍历供应商i时,判断当前解是否符合约束条件,以及是否为更优解,适当更新最优值与最优解。
- 如果儿子结点不是叶结点,符合约束条件并又可能存在更优解,则将儿子结点加入到活结点优先级队列中。
代码:
1 | // 最小重量机器设计问题 |