arxiv:https://arxiv.org/abs/1807.03748
code:https://github.com/jefflai108/Contrastive-Predictive-Coding-PyTorch
1 Introduce
作者提出了一种叫做“对比预测编码(CPC, Contrastive Predictive Coding)”的无监督方法,可以从高维数据中提取有用的 representation,这种 representation 学习到了对预测未来最有用的信息。
目前无监督学习存在的问题:
- 如何更好的从原始观测值中建模high-level representarion
- 理想情况下的学习的representation到底是什么样的?是否可以使用无监督学习进行理想的representation learning?
- 作者将无监督学习与预测编码的思想相结合,提出了是否学习到一些能对未来有很好预测效果的representation?
本文的工作如下:
- 将高维数据压缩到更紧凑的隐空间中,在其中条件预测更容易建模。
- 我们使用强大的自回归模型在这个隐空间中预测未来的许多步骤。
- 依靠噪声对比估计(Noise-Contrastive Estimation)$^{[12]}$来计算损失函数(和自然语言模型中的学习单词嵌入方式类似),从而可以对整个模型进行端到端的训练。
- 最终提出的Contrastive Predictive Codeing(CPC)方法可以用相同的机制在图像、语音、自然语言、强化学习等多个模态的数据上都能学习到高级信息。
2 Motivation && Intuitions
模型主要的Intuitions就是学习一种能够对高维信号不同部分的基础共享信息(underlying shared infomation)进行编码的representation,同时丢弃掉更底层的低级信息和噪声。在时间序列和高维的建模中,通过对能够进行预测的representation进行学习,会使其学习到更多的全局结构,作者将学习到的这种特征称为”slow features“。$^{[13]}$
预测高维数据的难点之一是均方误差和交叉熵这样的单峰损失效果不好,而如果使用一个强大的条件生成模型对每个细节进行重建,就会需要很大的计算量,并且会忽略了数据集$x$中的上下文关系$c$。(如一张图片包含上千位的信息,而最后的高级隐变量有可能仅仅是1024类别里10bit的一个类标签)。
因此如果是为了提取出$x$和$c$之间的共享信息(shared information),直接建模生成模型 $p(x|c)$ 并不是最佳的。
作者提出最大化 $x$(预测的未来)和上下文 $c$ (现在的环境)之间互信息的方式,定义如下:
$$
I(x ; c)=\sum_{x, c} p(x, c) \log \frac{p(x \mid c)}{p(x)} \tag{1}
$$
这里进一步解释一些互信息(mutual infomation),互信息实际上就是表示两个变量之间的相关性,上式也就是互信息的定义式的变形,$I(x;c)$表示 $x$ 与 $c$ 的关系,但具体是什么关系呢?可以看如下的推导:
最终的结果是 $H(x)-H(x|c)$,其中$H(x)$为$x$的熵,用来衡量$x$的不确定度,定义如下:
$$
H(x)=-\sum_x p(x)logp(x)
$$
而$I(x,c)=H(x)-H(x|c)$也就说明了$x$与$c$的互信息即表示由于 $c$ 的引入而使 $x$ 熵减小的量,也就是 $x$ 不确定度减小的量。
因此,放在论文中的含义来看,最大化$I(x;c)$也就是通过充分学习现在的上下文 $c$ 最大程度的减小了未来 $x$ 的不确定度,从而起到了预测的效果,所以所以CPC希望网络可以最大化 $x$ 和 $c$ 之间的互信息。
3 Method
3.1 Contrastive Predicting Coding
understanding-of-CPC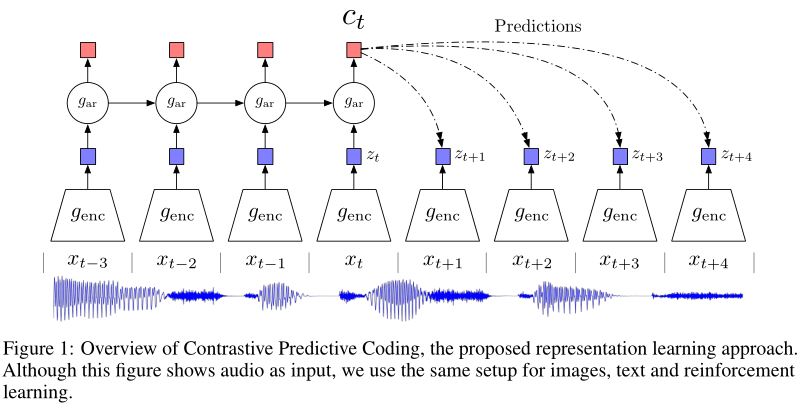
上图就是 CPC 的架构图(以语音信号为例),首先用非线性编码器 $g_{enc}$(如AutoEncoder或者CNN) 将分割的时间窗口上的每个观测值 $x_t$的进行 $z_t=g_{enc}(x_t)$ 映射,得到到representation vector,然后再将$z_t$以及潜空间中之前所有时刻的相关信息输入到一个自回归模型 $g_{ar}$中,生成当前时刻的上下文表示$c_t=g_{ar}(z_{≤t})$
如果要用当前的 $c$ 去预测 $k$ 个时刻后的 $z_{t+k}$ ,之前提到作者不采用生成模型 $p(x_{t+k}|c)$ 进行预测,而是最大化 $x_{t+k}$和 $c$ 之间的互信息使得预测的 $\hat{z}_{t+i}$ 与真实的 $z_{t+i}$ 尽可能的相似。 根据等式1,我们没办法控制互信息中的 $x$ 和 $c$ 的联合分布概率 $p(x,c)$,因此作者提出了一个密度比的概念,如下:$$
f_{k}\left(x_{t+k}, c_{t}\right) \propto \frac{p\left(x_{t+k} \mid c_{t}\right)}{p\left(x_{t+k}\right)} \tag {2}
$$
然后作者直接用线性矩阵 $W_1,W_2,\dots,W_k$乘以$c_t$来作为预测值(即$W_kc_t$),而$z_{t+k}^K$为真实值,用向量内积来衡量相似度,由此得到了论文中的如下函数来逼近密度比:
$$
f_{k}\left(x_{t+k}, c_{t}\right)=\exp \left(z_{t+k}^{T} W_{k} c_{t}\right) \tag{3}
$$
3.2 InfoNCE Loss
下面考虑如何对模型进行优化从而实现我们的目标,这里作者参考了NCE loss的思想提出了InfoNCE loss,定义如下:
$$ \mathcal{L}_{\mathrm{N}}=-\underset{X}{\mathbb{E}}\left[\log \frac{f_{k}\left(x_{t+k}, c_{t}\right)}{\sum_{x_{j} \in X} f_{k}\left(x_{j}, c_{t}\right)}\right] \tag{4} $$ 其中 $X={\{x_1,x_2,\dots,x_N\}} $ 是一组样本,这里面 $(x_{t+k},c_t$) 可以看成正样本对,$(x_j,c_t)$可以看成负样本对。**因此为了优化该损失,我们希望分子尽可能大,分母尽可能小。这也就符合我们对于 $x$ 和 $c$ 互信息的要求,即正样本对之间的互信息更大,负样本对之间的互信息更小。优化该损失,实际上就是最大化$x_{t+k}$ 和 $c_t$ 间的互信息。**等式4实际上是一个正确分类正样本的多分类交叉熵损失(这里可以用softmax理解,但并不一定是softmax)。现在考虑该损失的最佳情况,假设 $x_i$ 是 $c_t$ 预测的结果,即正样本,那么 $x_i$ 被采样的概率如下,这实际上也就是等式2中定义的 $f_k(x_{i},c_t)$的最优输出结果:
$$
\begin{aligned}
p\left(d=i \mid X, c_{t}\right) &=\frac{p\left(x_{i} \mid c_{t}\right) \prod_{l \neq i} p\left(x_{l}\right)}{\sum_{j=1}^{N} p\left(x_{j} \mid c_{t}\right) \prod_{l \neq j} p\left(x_{l}\right)} \
&=\frac{\frac{p\left(x_{i} \mid c_{t}\right)}{p\left(x_{i}\right)}}{\sum_{j=1}^{N} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}}
\end{aligned} \tag{5}
$$
可以看到 $f_k(x_{t+k},c_t)$ 确实与 $\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}$ 成比例,并且与负样本选择的数量 $N-1$ 无关,与前面所定义的密度比的概念相符合。
3.3 Estimating the MI with InfoNCE
虽然我们已经能够训练这个网络,但实际上我们可以具体推导 InfoNCE 和互信息之间的关系,以证明优化 InfoNCE loss 确实对在最大化互信息有帮助。由前面可以知道,$f_k(x_{t+k},c_t)$ 是由 $\frac{p(x_{t+k}|c_t)}{p(x_{t+k})}$ 决定,因此将其带入等式4中,并且将 $X$ 氛围正样本 $x_{t+k}$ 和负样本 $X_{neg}$ :
$$ \begin{aligned} \mathcal{L}_{\mathrm{N}}^{\mathrm{opt}} &=-\underset{X}{\mathbb{E}} \log \left[\frac{\frac{p\left(x_{t+k} \mid c_{t}\right)}{p\left(x_{t+k}\right)}}{\frac{p\left(x_{t+k} \mid c_{t}\right)}{p\left(x_{t+k}\right)}+\sum_{x_{j} \in X_{\mathrm{ncg}}} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}}\right] \\ &=\underset{X}{\mathbb{E}} \log \left[1+\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)} \sum_{x_{j} \in X_{\text {neg }}} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}\right] \\ & \approx \underset{X}{\mathbb{E}} \log \left[1+\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)}(N-1) \underset{x_{j}}{\mathbb{E}} \frac{p\left(x_{j} \mid c_{t}\right)}{p\left(x_{j}\right)}\right] \\ &=\underset{X}{\mathbb{E}} \log \left[1+\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)}(N-1)\right] \\ & \geq \underset{X}{\mathbb{E}} \log \left[\frac{p\left(x_{t+k}\right)}{p\left(x_{t+k} \mid c_{t}\right)} N\right] \\ &=-I\left(x_{t+k}, c_{t}\right)+\log (N) \end{aligned} $$所以最终得到:
$$
I\left(x_{t+k}, c_{t}\right)\geq \log (N)-L_N^{opt}
$$
优化InfoNCE(最小化$L_N^{opt}$)也就是最大化 $X_{t+k}$ 和 $c_t$ 之间的互信息的下限,并且 $N$ 越大,上面第三步中的约等于就越准确。
InfoNCE也与MINE有关$^{[54]}$,不失一般性的定义 $f(x,c)=e^{F(x,c)}$:
$$ \begin{aligned} \underset{X}{\mathbb{E}}\left[\log \frac{f(x, c)}{\sum_{x_{j} \in X} f\left(x_{j}, c\right)}\right]&=\underset{(x, c)}{\mathbb{E}}[F(x, c)]-\underset{(x, c)}{\mathbb{E}}\left[\log \sum_{x_{j} \in X} e^{F\left(x_{j}, c\right)}\right] \\ &= \underset{(x, c)}{\mathbb{E}}[F(x, c)]-\underset{(x, c)}{\mathbb{E}}\left[\log \left(e^{F(x, c)}+\sum_{x_{j} \in X_{\text {neg }}} e^{F\left(x_{j}, c\right)}\right)\right] \\ & \leq \underset{(x, c)}{\mathbb{E}}[F(x, c)]-\underset{c}{\mathbb{E}}\left[\log \sum_{x_{j} \in X_{\mathrm{neg}}} e^{F\left(x_{j}, c\right)}\right] \\ & =\underset{(x, c)}{\mathbb{E}}[F(x, c)]-\underset{c}{\mathbb{E}}\left[\log \frac{1}{N-1} \sum_{x_{j} \in X_{\text {neg }}} e^{F\left(x_{j}, c\right)}+\log (N-1)\right] \end{aligned} $$而MINE的定义为:
$$ I \widehat{(X ; Z)}_{n}=\sup _{\theta \in \Theta} \mathbb{E}_{\mathbb{P}_{X Z}^{(n)}}\left[T_{\theta}\right]-\log \left(\mathbb{E}_{\mathbb{P}_{X}^{(n)} \otimes \hat{\mathbb{P}}_{Z}^{(n)}}\left[e^{T_{\theta}}\right]\right) $$ 最终推导的结果几乎等价于MINE估计器,只是多了一个常数 $\underset{c}{\mathbb{E}}[\log (N-1)]$ 。作者声明,当面临困难任务时,InfoNCE与MINE表现都很好,而如果目标很容易根据上下文进行预测的简答任务,则MINE会变得不稳定。4 Experiments
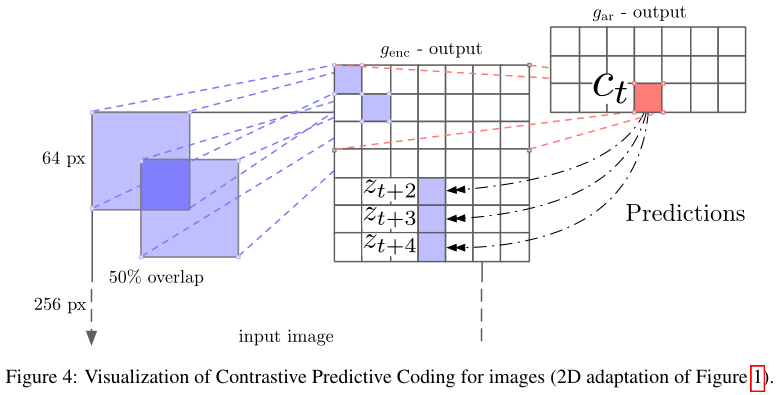
CPC在计算机视觉领域的用法
相关知识补充:
(1)表征学习(Representation Learning):学习数据的表征,以便在构建分类器或其他预测器时更容易提取有用的信息,无监督学习也属于表征学习。
参考链接:https://www.jiqizhixin.com/graph/technologies/64d4c374-6061-46cc-8d29-d0a582934876
(2)自回归模型(Autoregressive Model,AR模型):是统计上一种处理时间序列的方法,用同一变数,例如$x$的之前各期,即$x_1$至$x_{t-1}$来预测本期$x_t$的表现,并假设它们为线性关系。这是从回归分析的线性回归发展而来,只不过不是$x$预测$y$,而是用$x$预测$x$(自己),所以叫做自回归。
定义:
$$
X_{t}=c+\sum_{i=1}^{p} \varphi_{i} X_{t-i}+\varepsilon_{t}
$$
其中:$c$是常数项;$\varepsilon_{t}$被假设为平均数等于0,标准差等于$\sigma$的随机误差值;$\varepsilon _{t}$被假设为对于任何的$t$都不变。
(3)隐空间(latent space):GAN的输入空间,指隐变量$z$的样本空间,”隐变量”可以理解为控制数据$X$生成的”幕后之手“。在统计机器学习中,隐变量生成式模型“生成”数据$X$的背后逻辑是,通过建模联合分布$p_θ(z,X)$ ,再从中采样得到 $(z,X)$ 对。具体操作是,为隐变量选择一个容易采样的分布,如高斯,再通过神经网络建模$p_θ(X|z)$,从而采样得到生成的数据。
(4)互信息(Mutual Information):指变量间的相关性,通常用$I(X;Y)$表示$X$和$Y$之间的互信息:
$$
I(X ; Y)=\sum_{x \in X} \sum_{y \in Y} p(x, y) \log \frac{p(x \mid y)}{p(x)}
$$
$I(X;Y)$越大说明两者关系越密切。
参考链接:https://www.cnblogs.com/gatherstars/p/6004075.html
文中定义的互信息为:
$$
I(x, c) =\sum_{x, c} p(x, c) \log \frac{p(x \mid c)}{p(x)}
$$
表示由于$c$的引入使得$x$不确定度减小的量,如下推导:
其中$H(x)$为$x$的熵,用来衡量$x$的不确定度,定义如下:
$$
H(x)=-\sum_x p(x)logp(x)
$$
由$I(x,c)=H(x)-H(x|C)$也就说明了$x$与$c$的互信息即表示由于$c$的引入而使$x$熵减小的量,也就是$x$不确定度减小的量。
(5)对比损失(Contrastive Loss):
(6)NCE Loss
https://blog.csdn.net/weixin_40901056/article/details/88568344
(7)softmax函数:
softmax用于多分类过程中,它将多个神经元的输出,映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类。
假设我们有一个数组,V,Vi表示V中的第i个元素,那么这个元素的softmax值就是:
$$ S_{i}=\frac{e^{i}}{\sum_{j} e^{j}} $$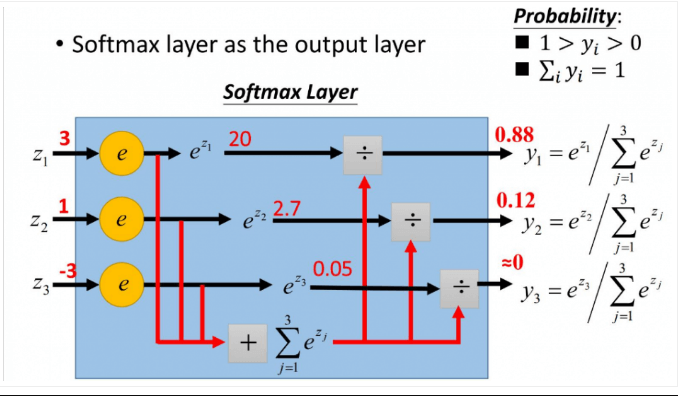
如上图,将原来输出的 3,1,-3 通过softmax函数作用,映射成为(0,1)的值,而这些值的累和为1(满足概率的性质),那么我们就可以将它理解成概率,在最后选取输出结点的时候,我们就可以选取概率最大(也就是值对应最大的)结点,作为我们的预测目标。
(8)各种熵:
https://zhuanlan.zhihu.com/p/35423404
https://www.jianshu.com/p/2ea0406d0793
参考链接:
https://zhuanlan.zhihu.com/p/129076690
https://zhuanlan.zhihu.com/p/75517749
https://zhuanlan.zhihu.com/p/137076811
参考文献:
[12] Michael Gutmann and Aapo Hyvärinen. Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pages 297–304, 2010.
[13] Laurenz Wiskott and Terrence J Sejnowski. Slow feature analysis: Unsupervised learning of invariances. Neural computation, 14(4):715–770, 2002.
[54] Ishmael Belghazi, Sai Rajeswar, AristideN Baratin, R Devon Hjelm, and Aaron Courville. Mine: Mutual information neural estimation. 2018.